练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．若圆（x-1）2+（y+1）2=16上的点P到直线4x+3y=11的距离等于2，点P的个数是（　　）
    A．只有一个B．两个C．有三个D．四个

    分析 求出圆心到直线的距离，进而可得满足条件的P点的个数．

    解答 解：圆（x-1）2+（y+1）2=16的圆心（1，-1）到直线4x+3y=11的距离d=$\frac{|4-3-11|}{5}$=2，
    圆（x-1）2+（y+1）2=16的半径为4，
    故圆上的点P到直线4x+3y=11的距离等于2的个数有3个，
    故选：C．

    点评 本题考查的知识点是直线与圆的位置关系，点到直线的距离公式，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

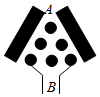    8．将一个半径适当的小球从如图所示的A入口处，向下自由下落．小球在下落的过程中，将3次遇到黑色障碍物，每次遇到黑色障碍物时，向左、右两边下落的概率都是$\frac{1}{2}$，最后通过黑色区域．
    （1）求小球从B出口通过的概率P（B）；
    （2）在容器入口处依次放入4个小球，记ξ为从B出口通过的小球个数，求ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

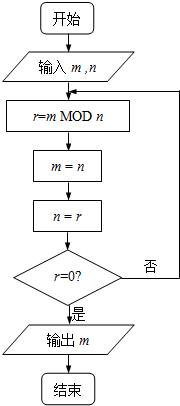    9．如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”，执行该程序框图（图中“m MOD n”表示m除以n的余数），若输入的m，n分别为495，135，则输出的m=（　　）
    A．0B．5C．45D．90

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

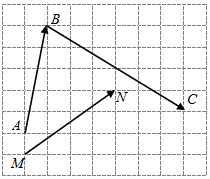    6．向量$\overrightarrow{AB}$，$\overrightarrow{BC}$，$\overrightarrow{MN}$在正方形网格中的位置如图所示，若$\overrightarrow{MN}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{BC}$（λ，μ∈R），则$\frac{λ}{μ}$=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知数列{an}中an≠0，若a1=2，2an+1•an=n（an-an+1）+an，则数列{an}的通项公式为an=$\frac{2n}{4n-3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

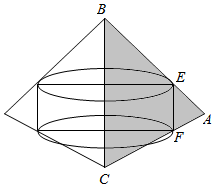    3．△ABC中，E，F分别为AB，AC的中点，以BC为边所在直线为轴旋转，四边形BCFE和△AEF旋转所得的几何体的体积分别为V1，V2，则（　　）
    A．V1＞V2B．V1＜V2
    C．V1=V2D．V1，V2大小关系不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知{an}是等差数列．
    （1）若a1+a3+a7+a9+a20=55，求a3+a13的值．
    （2）若a3+a7+a11=18，a3a7a11=120，求{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．计算：$\frac{4co{s}^{2}（-\frac{15π}{4}）}{tan（-\frac{11π}{3}）-\sqrt{2}sin（\frac{21π}{4}）}$的值为$\sqrt{3}-1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．设实数x、y满足x2+（y-1）2=1，当x+y+d≥0恒成立时，d的取值范围是d≥1+$\sqrt{2}$．

    查看答案和解析>>

    同步练习册答案