Question

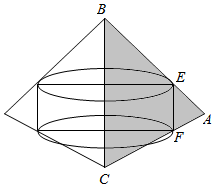
3．△ABC中，E，F分别为AB，AC的中点，以BC为边所在直线为轴旋转，四边形BCFE和△AEF旋转所得的几何体的体积分别为V₁，V₂，则（　　）

• A． V₁＞V₂
• B． V₁＜V₂
• C． V₁=V₂
• D． V₁，V₂大小关系不确定

Answer 1

分析 求出三角形ABC绕BC旋转所得几何体的体积，把四边形BCFE绕BC旋转所得几何体的体积转化为两个圆锥及一个圆柱的体积和，求出V₁，用总体积减去V₁得V₂，则答案可求．

解答 解：如图
设BC=a，A到BC边的距离为h，
则EF=$\frac{1}{2}a$，E到BC边的距离为$\frac{1}{2}h$，
则旋转后所得旋转体的体积为$\frac{1}{3}aπ{h}^{2}$，
四边形BCFE绕BC旋转后所得几何体的体积为：$\frac{1}{3}•π（\frac{1}{2}h）^{2}•\frac{1}{2}a+π（\frac{1}{2}h）^{2}•\frac{1}{2}a$=$\frac{4}{3}π•\frac{1}{4}{h}^{2}•\frac{1}{2}a=\frac{1}{6}πa{h}^{2}$，
∴${V}_{1}=\frac{1}{6}πa{h}^{2}$，
则${V}_{2}=\frac{1}{3}πa{h}^{2}-\frac{1}{6}πa{h}^{2}=\frac{1}{6}πa{h}^{2}={V}_{1}$，
故选：C．

点评 本题考查柱、锥、台体的体积的求法，考查空间想象能力和思维能力，是中档题．