
分析 ①利用换元法求解即可;
②根据定义,用代入法求解;
③根据抽象函数,把x换为-x,解方程组即可;
④根据偶函数的性质得出f(0)=0,再令y=-x,得出函数解析式.
解答 解:(1)已知f($\sqrt{x}$-1)=x-2$\sqrt{x}$,
令t=$\sqrt{x}$-1,t≥-1,
∴x=(t+1)2,f(t)=(t+1)2-2(t+1)=t2-1,
∴f(x)=x2-1,(x≥-1);
(2)设f(x)=ax2+bx+c,
∵f(0)=0,
∴c=0;
∵f(x+1)=f(x)+x+1,
∴ax2+(2a+b)x+a+b=ax2+(b+1)x+1,
∴a=b=$\frac{1}{2}$,f(x)=$\frac{1}{2}$x2+$\frac{1}{2}$x;
(3)f(x)满足f(x)+2f(-x)=$\frac{1}{1+x}$,
∴f(-x)+2f(x)=$\frac{1}{1-x}$,
∴f(x)=$\frac{3x+1}{3(1{-x}^{2})}$;
(4)已知f(x)为偶函数,且对于任意实数x,y,都有f(x+y)=f(x)+f(y)+xy,
令x=y=0,
∴f(0)=0,令y=-x,
∴f(0)=f(x)+f(-x)-x2,
∴f(x)=x2.
点评 考查了换元法,代入法,解方程组的方法求解函数解析式.


科目:高中数学 来源: 题型:解答题
 某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.
某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 300e2mg/L | B. | 300emg/L | C. | $\frac{300}{e^2}$mg/L | D. | $\frac{300}{e}$mg/L |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
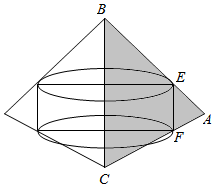 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2大小关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9-4$\sqrt{5}$ | B. | 4$\sqrt{5}$-9 | C. | 5$\sqrt{2}$-9 | D. | 9+4$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -4 | C. | -$\frac{4}{5}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com