
 某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.
某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.分析 (Ⅰ)设一次抽奖抽中i等奖的概率为Pi(i=1,2),没有中奖的概率为P0,由此能求出该顾客两次抽奖中恰有一次中奖的概率.
(Ⅱ)X的可能取值为0,50,100,150,200,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)设一次抽奖抽中i等奖的概率为Pi(i=1,2),没有中奖的概率为P0,
则P1+P2=$\frac{3}{20}+\frac{5}{20}$=$\frac{2}{5}$,即中奖的概率为$\frac{2}{5}$,
∴该顾客两次抽奖中恰有一次中奖的概率为:
P=${C}_{2}^{1}×\frac{2}{5}×\frac{3}{5}$=$\frac{12}{25}$.
(Ⅱ)X的可能取值为0,50,100,150,200,
P(X=0)=$\frac{9}{25}$,
P(X=50)=${C}_{2}^{1}×\frac{5}{20}×\frac{3}{5}$=$\frac{3}{10}$,
P(X=100)=$\frac{5}{20}×\frac{5}{20}+{C}_{2}^{1}×\frac{3}{20}×\frac{3}{5}$=$\frac{97}{400}$,
P(X=150)=${C}_{2}^{1}×\frac{3}{20}×\frac{5}{20}$=$\frac{3}{40}$,
P(X=200)=$\frac{3}{20}×\frac{3}{20}$=$\frac{9}{400}$,
∴X的分布列为:
| X | 0 | 50 | 100 | 150 | 200 |
| P | $\frac{9}{25}$ | $\frac{3}{10}$ | $\frac{97}{400}$ | $\frac{3}{40}$ | $\frac{9}{400}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
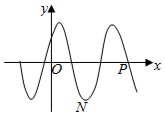 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )| A. | $[\frac{π}{8},\frac{5π}{8}]$ | B. | $[-\frac{7π}{8},-\frac{3π}{8}]$ | C. | $[\frac{9π}{4},\frac{21π}{8}]$ | D. | $[\frac{9π}{8},\frac{33π}{8}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
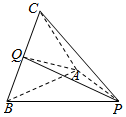 如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com