
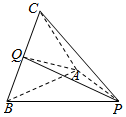
 如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.分析 (1)由题意得到三角形ABC为等边三角形,由Q为BC中点,得到AQ垂直于BC,同理得到三角形BPC为等边三角形,得到PQ垂直于BC,由AQ与QC交于Q,得到BC与平面APQ垂直,而AP属于平面PAQ,即可得到PA与BC垂直;
(2)设点Q到平面PAC的距离为h,根据VQ-ACP=VC-APQ,利用体积法求出h,即为点Q到平面PAC的距离.
解答 (1)证明:∵在△ABC中,BC=AB,∠CBA=60°,
∴△ABC为等边三角形,
∵Q为BC的中点,
∴AQ⊥BC,
同理在等边△BPC中,PQ⊥BC,
∵QA∩QC=Q,
∴BC⊥平面PAQ,
∵AP?平面PAQ,
∴BC⊥PA;
(2)设点Q到平面PAC的距离为h,由(1)得QA=QP=$\sqrt{3}$,
∵AP=2,
∴S△QPA=$\frac{1}{2}$×2×$\sqrt{2}$=$\sqrt{2}$,
∵BC⊥平面PAQ,且CQ=1,
∴VC-PAQ=$\frac{1}{3}$×$\sqrt{2}$×1=$\frac{\sqrt{2}}{3}$,
∵AC=AP=PC=2,
∴S△PAC=$\frac{1}{2}$×2×2×sin60°=$\sqrt{3}$,
∴VQ-PAC=$\frac{1}{3}$×$\sqrt{3}$×h,
∵VC-PAQ=VQ-PAC,
∴$\frac{\sqrt{2}}{3}$=$\frac{1}{3}$×$\sqrt{3}$×h,
解得:h=$\frac{\sqrt{6}}{3}$,
则点Q到平面PAC的距离为$\frac{\sqrt{6}}{3}$.
点评 此题考查了点、线、面之间的距离,等边三角形的判定与性质,以及直线与平面垂直的判定与性质,熟练掌握判定与性质是解本题的关键.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 3或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $-\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.
某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{7}{20}$ | C. | $\frac{9}{20}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 300e2mg/L | B. | 300emg/L | C. | $\frac{300}{e^2}$mg/L | D. | $\frac{300}{e}$mg/L |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9-4$\sqrt{5}$ | B. | 4$\sqrt{5}$-9 | C. | 5$\sqrt{2}$-9 | D. | 9+4$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com