
| A. | 3 | B. | 4 | C. | 5 | D. | 3或5 |
分析 由sinB=sin2A=2sinAcosA,由正弦定理$\frac{a}{snA}=\frac{b}{sinB}$,可知b=2acosA,再由余弦定理可得到关于c的一元二次方程,解得c的值.
解答 解:在△ABC中,由已知条件可知:sinB=sin2A=2sinAcosA;
由正弦定理$\frac{a}{sinA}=\frac{b}{sinB}$,b=$\frac{asinB}{sinA}$,
∴b=2acosA
cosA=$\frac{\sqrt{6}}{3}$
余弦定理$cosA=\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$
整理可知:c2-8c+15=0
解得c1=3或c2=5
当c=3时,a=c=3时,
则A=C,又B=2A,A+B+C=180°,
得A=C=45°,B=90°,
则三角形ABC为等腰直角三角形,b=3$\sqrt{2}$与b=2$\sqrt{6}$矛盾,
故c=5,
故选C.
点评 本题主要考察正弦定理和余弦定理,最后要验证是否满足三角形.属于中档题


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $[{-\frac{π}{4},\frac{π}{4}}]$ | B. | $[{-\frac{π}{2},0}]$ | C. | $[{0,\frac{π}{2}}]$ | D. | $[{\frac{π}{4},\frac{3π}{4}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
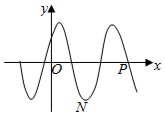 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )| A. | $[\frac{π}{8},\frac{5π}{8}]$ | B. | $[-\frac{7π}{8},-\frac{3π}{8}]$ | C. | $[\frac{9π}{4},\frac{21π}{8}]$ | D. | $[\frac{9π}{8},\frac{33π}{8}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
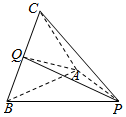 如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
如图,在三棱锥P-ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com