
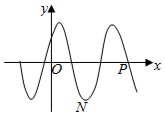
 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )| A. | $[\frac{π}{8},\frac{5π}{8}]$ | B. | $[-\frac{7π}{8},-\frac{3π}{8}]$ | C. | $[\frac{9π}{4},\frac{21π}{8}]$ | D. | $[\frac{9π}{8},\frac{33π}{8}]$ |
分析 解法一:根据题意,求出函数f(x)的解析式,得出f(x)的递减区间,再判定4个选项中是否为f(x)的单调减区间.
解法二:求出函数f(x)的周期T=π,判定选项D区间长度是3T,f(x)不是单调减函数,由此得出结论.
解答 解:(法一)根据题意,设函数f(x)=Acos(ωx+φ)的周期为T,
则$\frac{3}{4}$T=$\frac{11π}{8}$-$\frac{5π}{8}$=$\frac{3π}{4}$,解得T=π,
∴ω=2;
又x=$\frac{5π}{8}$,
∴2×$\frac{5π}{8}$+φ=π+kπ,k∈Z;
解得φ=-$\frac{π}{4}$+kπ,k∈Z;,
又|φ|<$\frac{π}{2}$,
∴φ=-$\frac{π}{4}$,
∴f(x)=Acos(2x-$\frac{π}{4}$);
令2kπ≤2x-$\frac{π}{4}$≤π+2kπ,k∈Z,
∴$\frac{π}{8}$+kπ≤x≤$\frac{5π}{8}$+kπ,k∈Z,
当k=0时,x∈[$\frac{π}{8}$,$\frac{5π}{8}$],f(x)是单调减函数,A满足题意;
当k=-1时,x∈[-$\frac{7π}{8}$,-$\frac{3π}{8}$],f(x)是单调减函数,B满足题意;
当k=2时,x∈[$\frac{17π}{8}$,$\frac{25π}{8}$],f(x)是单调减函数,又[$\frac{9π}{4}$,$\frac{21π}{8}$]?[$\frac{17π}{8}$,$\frac{25π}{8}$],∴C满足题意;
当k=1时,x∈[$\frac{9π}{8}$,$\frac{17π}{8}$],f(x)是单调减函数,又[$\frac{9π}{8}$,$\frac{17π}{8}$]?[$\frac{9π}{8}$,$\frac{33π}{8}$],∴D不满足题意.
(法二)根据题意,设函数f(x)=Acos(ωx+φ)的周期为T,
则$\frac{3}{4}$T=$\frac{11π}{8}$-$\frac{5π}{8}$=$\frac{3π}{4}$,解得T=π;
又选项D中,区间长度为$\frac{33π}{8}$-$\frac{9π}{8}$=3π,
∴f(x)在区间[$\frac{9π}{8}$,$\frac{33π}{8}$]上不是单调减函数.
故选:D.
点评 本题考查了余弦函数y=Acos(ωx+φ)的图象与性质的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,$\sqrt{{3}^{{x}_{0}}+1}$>2 | B. | ?x0∈R,$\sqrt{{3}^{{x}_{0}}+1}$≥2 | C. | ?x∈R,$\sqrt{{3}^{x}+1}$>2 | D. | ?x∈R,$\sqrt{{3}^{x}+1}$≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 3或5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y-1)2=8 | B. | x2+(y+1)2=8 | C. | (x-1)2+(y+1)2=8 | D. | (x+1)2+(y-1)2=8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -15 | B. | 15 | C. | 20 | D. | -20 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $-\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.
某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 300e2mg/L | B. | 300emg/L | C. | $\frac{300}{e^2}$mg/L | D. | $\frac{300}{e}$mg/L |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com