
| A. | y3=x2z | B. | y3=xz2 | C. | y2=xz | D. | 2y3=3xz2 |
分析 利用换底公式化简可得$lo{g}_{\frac{x}{y}}$$\frac{y}{z}$+4$lo{g}_{\frac{y}{z}}$$\frac{x}{y}$=4,从而解得$lo{g}_{\frac{x}{y}}$$\frac{y}{z}$=2.
解答 解:∵log2($\frac{x}{z}$)•[log${\;}_{(\frac{x}{y})}$2+log${\;}_{(\frac{y}{z})}$16]=9,
∴(log2$\frac{x}{y}$+log2$\frac{y}{z}$)•[log${\;}_{(\frac{x}{y})}$2+log${\;}_{(\frac{y}{z})}$16]=9,
∴log2$\frac{x}{y}$•log${\;}_{(\frac{x}{y})}$2+log2$\frac{x}{y}$log${\;}_{(\frac{y}{z})}$16+log2$\frac{y}{z}$log${\;}_{(\frac{x}{y})}$2+log2$\frac{y}{z}$log${\;}_{(\frac{y}{z})}$16=9,
∴5+log2$\frac{y}{z}$log${\;}_{(\frac{x}{y})}$2+log2$\frac{y}{z}$log${\;}_{(\frac{y}{z})}$16=9,
∴log2$\frac{y}{z}$log${\;}_{(\frac{x}{y})}$2+log2$\frac{x}{y}$log${\;}_{(\frac{y}{z})}$16=4,
∴$lo{g}_{\frac{x}{y}}$$\frac{y}{z}$+4$lo{g}_{\frac{y}{z}}$$\frac{x}{y}$=4,
解得,$lo{g}_{\frac{x}{y}}$$\frac{y}{z}$=2,
故$\frac{y}{z}$=$\frac{{x}^{2}}{{y}^{2}}$,
故y3=x2z,
故选:A.
点评 本题考查了对数运算的应用及学生的化简运算能力的应用.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:选择题
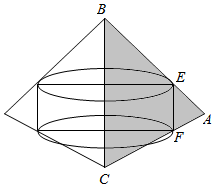 △ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )
△ABC中,E,F分别为AB,AC的中点,以BC为边所在直线为轴旋转,四边形BCFE和△AEF旋转所得的几何体的体积分别为V1,V2,则( )| A. | V1>V2 | B. | V1<V2 | ||
| C. | V1=V2 | D. | V1,V2大小关系不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -4 | C. | -$\frac{4}{5}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{15}{16}$) | B. | ($\frac{15}{16}$,1) | C. | (1,$\frac{16}{15}$) | D. | (1,$\frac{5}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com