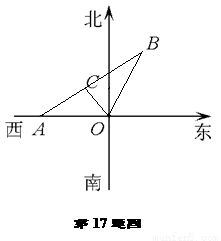
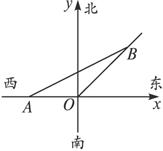
某市现有自市中心O通往正西和东北方向的两条主要公路,为了解决交通拥挤问题,市政府决定修一条环城路,分别在通往正西和东北方向的公路上选取A、B两点,使环城公路在A、B间为线段,要求AB环城路段与中心O的距离为10 km,且使A、B间的距离|AB|最小,请你确定A、B两点的最佳位置(不要求作近似计算)
分析:先以O为原点,正东方向为x轴的正半轴,正北方向为y轴的正半轴,建立直角坐标系.设A(-a,0)、B(b,b),则可得直线AB的方程,再根据点到直线的距离公式可得a
2b
2=100(a
2+2b
2+2ab),进而求得ab的范围,再根据两点间的距离求得|AB|=
,进而可得|AB|的范围及最小值.当|AB|取最小值时可求得a,b的值,进而求出|OA|和|OB|,确定A,B的位置.
解答:
解:以O为原点,正东方向为x轴的正半轴,正北方向为y轴的正半轴,建立如下图所示的坐标系.
设A(-a,0)、B(b,b)(其中a>0,b>0),
则AB的方程为y=
•x+,
即bx-(a+b)y+ab=0.
∴a
2b
2=100(a
2+2b
2+2ab)≥100(2
+2ab)
=200(1+
)ab.
∵ab>0,
∴ab≥200(
+1).
当且仅当“a
2=2b
2”时等号成立,
而|AB|=
=
,
∴|AB|≥20(
+1).
当a
2=2b
2,
ab=10
,
时,|AB|取最小值,
即a=10
,
b=10
此时|OA|=a=10
,
|OB|=10
,
∴A、B两点的最佳位置是离市中心O均为10
km处.
点评:本题主要考查了平面几何的性质在实际中的应用.要熟练掌握点与直线、直线与直线、直线与曲线的关系.

 解:以O为原点,正东方向为x轴的正半轴,正北方向为y轴的正半轴,建立如下图所示的坐标系.
解:以O为原点,正东方向为x轴的正半轴,正北方向为y轴的正半轴,建立如下图所示的坐标系.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案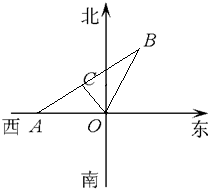 如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.
如图某市现有自市中心O通往正西和北偏东30°方向的两条主要公路,为了解决该市交通拥挤问题,市政府决定修建一条环城公路.分别在通往正西和北偏东30°方向的公路上选用A、B两点,使环城公路在A、B间为直线段,要求AB路段与市中心O的距离为10km,且使A、B间的距离|AB|最小.请你确定A、B两点的最佳位置.