
【题目】已知各项不为零的数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.
(1)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值;
的值;
(2)若![]() 成等差数列,
成等差数列,
①求数列![]() 的通项公式;
的通项公式;
②在![]() 与
与![]() 间插入
间插入![]() 个正数,共同组成公比为
个正数,共同组成公比为![]() 的等比数列,若不等式
的等比数列,若不等式![]() 对任意的
对任意的![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)依据题设条件建立方程,通过解方程组进行分析求解;(2)先依据题设条件运用等差数列的定义建立方程求出参数![]() ,再借助数列的前
,再借助数列的前![]() 项和与通项之间的关系求出数列的通项公式;(3)依据题设条件运用两边取对数的方法将问题进行等价转化,然后将参数进行分离,构造函数运用函数思想及导数知识分析求解:
项和与通项之间的关系求出数列的通项公式;(3)依据题设条件运用两边取对数的方法将问题进行等价转化,然后将参数进行分离,构造函数运用函数思想及导数知识分析求解:
解:(1)当![]() 时,
时, ![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() ,
,
由![]() 得
得![]() ,即
,即![]() ,解得:
,解得: ![]() 。
。
(2)由![]() 得
得![]() ,故
,故![]() ,
, ![]() ,所以
,所以![]() ,
,
当![]() 时,
时, ![]() ,
,
因为![]() ,所以
,所以![]()
故数列![]() 的所有奇数项组成以
的所有奇数项组成以![]() 为公差的等差数列,
为公差的等差数列,
其通项公式![]() ,
,
同理,数列![]() 的所有偶数项组成以
的所有偶数项组成以![]() 为首项
为首项![]() 为公差的等差数列,
为公差的等差数列,
其通项公式是![]()
所以数列![]() 的通项公式是
的通项公式是![]()
(3)![]() ,在
,在![]() 与
与![]() 间插入
间插入![]() 个正数,组成公比为
个正数,组成公比为![]() 的等比数列,故有
的等比数列,故有![]() ,
,
即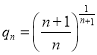 ,
,
所以![]() ,即
,即![]() ,两边取对数得
,两边取对数得![]() ,
,
分离参数得 恒成立
恒成立
令![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
令![]() ,
, ![]() ,则
,则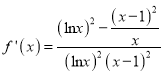 ,
,
下证![]() ,
, ![]() ,
,
令![]() , 则
, 则![]() ,所以
,所以![]() ,
,
即![]() ,用
,用![]() 替代
替代![]() 可得
可得![]() ,
, ![]() ,
,
所以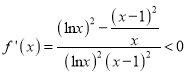 ,所以
,所以![]() 在
在![]() 上递减,
上递减,
所以![]()


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】已知Sn为数列{an}的前n项和,且an>0,an2+an=2Sn .
(1)求数列{an}的通项公式;
(2)令bn= ![]() ,记Tn=b12b32…b2n﹣12 , 求证:Tn≥
,记Tn=b12b32…b2n﹣12 , 求证:Tn≥ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是直角△ABC斜边BC上一点,AC= ![]() DC.
DC. 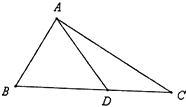
(Ⅰ)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD= ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )离y轴最近的零点与最大值均在抛物线y=﹣
)离y轴最近的零点与最大值均在抛物线y=﹣ ![]() x2+
x2+ ![]() x+1上,则f(x)=( )
x+1上,则f(x)=( )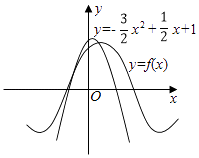
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】本市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产![]() ,
, ![]() ,
, ![]() 三种玩具共100个,且
三种玩具共100个,且![]() 种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
种玩具至少生产20个,每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如表:
玩具名称 |
|
|
|
工时(分钟) | 5 | 7 | 4 |
利润(元) | 5 | 6 | 3 |
(Ⅰ)用每天生产![]() 种玩具个数
种玩具个数![]() 与
与![]() 种玩具
种玩具![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(Ⅱ)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() 的离心率为
的离心率为 ![]() ,焦距为
,焦距为 ![]() ,抛物线C2:x2=2py(p>0)的焦点F是椭圆C1的顶点. (Ⅰ)求C1与C2的标准方程;
,抛物线C2:x2=2py(p>0)的焦点F是椭圆C1的顶点. (Ⅰ)求C1与C2的标准方程;
(Ⅱ)C1上不同于F的两点P,Q满足 ![]() ,且直线PQ与C2相切,求△FPQ的面积.
,且直线PQ与C2相切,求△FPQ的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个非零向量 ![]() 、
、 ![]() 不共线.
不共线.
(1)若 ![]() =
= ![]() +
+ ![]() ,
, ![]() =2
=2 ![]() +8
+8 ![]() ,
, ![]() =3(
=3( ![]() ﹣
﹣ ![]() ),求证:A、B、D三点共线;
),求证:A、B、D三点共线;
(2)求实数k使k ![]() +
+ ![]() 与2
与2 ![]() +k
+k ![]() 共线.
共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷,卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数![]() 是8的整数倍时,均可采用此方法求解,如图,是解决这类问题的程序框图,若输入
是8的整数倍时,均可采用此方法求解,如图,是解决这类问题的程序框图,若输入![]() ,则输出的结果为( )
,则输出的结果为( )
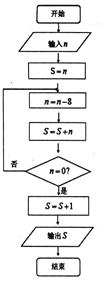
A. 120 B. 121 C. 112 D. 113
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com