练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜ ）离y轴最近的零点与最大值均在抛物线y=﹣ x2+ x+1上，则f（x）=（ ）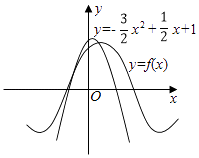

    A.
    B.

    C.
    D.

    【答案】C
    【解析】解：根据题意，函数f（x）离y轴最近的零点与最大值均在抛物线 上，
    令y=0，得﹣ x2+ x+1=0，
    解得x=﹣ 或x=1；
    ∴点（﹣ ，0）在函数f（x）的图像上，
    ∴﹣ ω+φ=0，即φ= ω①；
    又令ωx+φ= ，得ωx= ﹣φ②；
    把①代入②得，x= ﹣ ③；
    令y=1，得﹣ x2+ x+1=1，
    解得x=0或x= ；
    即 ﹣ = ，
    解得ω= π，
    ∴φ= ω= ，
    ∴f（x）=sin（ x+ ）．
    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知方程x2+y2﹣2x﹣4y+m=0．
    （1）若此方程表示圆，求m的取值范围；
    （2）若（1）中的圆与直线x+2y﹣4=0相交于M、N两点，且OM⊥ON（O为坐标原点），求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市为了满足市民出行的需要和节能环保的要求，在公共场所提供单车共享服务，某部门为了对该城市共享单车进行监管，随机选取了位市民对共享单车的情况逬行问卷调査，并根根据其满意度评分值（滿分分）制作的茎叶图如图所示：

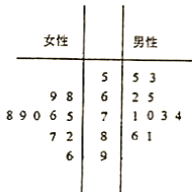
    （1）分别计算男性打分的平均数和女性打分的中位数；

    （2）从打分在分以下（不含分）的市民抽取人，求有女性被抽中的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】将函数y=sinx的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得的图象向左平移 个单位，得到的图象对应的解析式是（ ）
    A.y=sin（2x+ ）
    B.y=sin（ x+ ）
    C.y=sin（ x+ ）
    D.y=sin（2x+ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列的前n项和， 是等差数列，且.

    （Ⅰ）求数列的通项公式；

    （Ⅱ）令.求数列的前n项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图， 为圆的直径，点， 在圆上， ，矩形和圆所在的平面互相垂直，已知， ．

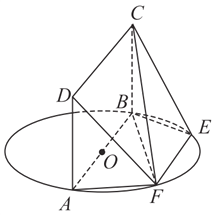
    （Ⅰ）求证：平面平面；

    （Ⅱ）求直线与平面所成角的大小；

    （Ⅲ）当的长为何值时，二面角的大小为．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项不为零的数列的前项和为，且， ， ．

    （1）若成等比数列，求实数的值；

    （2）若成等差数列，

    ①求数列的通项公式；

    ②在与间插入个正数，共同组成公比为的等比数列，若不等式对任意的恒成立，求实数的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（sinx+cosx）2+2cos2x﹣2．
    （1）求函数f（x）的最小正周期及单调递增区间；
    （2）当x∈[ ， ]时，求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣ ．
    （1）判断函数f（x）的奇偶性，并加以证明；
    （2）用定义证明函数f（x）在区间[1，+∞）上为增函数；
    （3）若函数f（x）在区间[2，a]上的最大值与最小值之和不小于 ，求a的取值范围．

    查看答案和解析>>

    同步练习册答案