【题目】已知方程x2+y2﹣2x﹣4y+m=0．
（1）若此方程表示圆，求m的取值范围；
（2）若（1）中的圆与直线x+2y﹣4=0相交于M、N两点，且OM⊥ON（O为坐标原点），求m的值．
【答案】
（1）解：由方程x2+y2﹣2x﹣4y+m=0变形为（x﹣1）2+（y﹣2）2=5﹣m．∵此方程表示圆，∴5﹣m＞0，解得m＜5，故m的取值范围是（﹣∞，5）
（2）解：设M（x1，y1），N（x2，y2）．
联立 
化为5y2﹣16y+8+m=0，
∵直线与圆相交，∴△=162﹣20（8+m）＞0，化为 
．
∴y1+y2= 
， 
．
∵ 
，∴ 
=0，
又x1x2=（4﹣2y1）（4﹣2y2）=16﹣8（y1+y2）+4y1y2，
∴5y1y2﹣8（y1+y2）+16=0，
∴8+m﹣ 
+16=0，
解得m= 
，满足 ，
故m=
【解析】（1）由方程x2+y2﹣2x﹣4y+m=0配方为（x﹣1）2+（y﹣2）2=5﹣m．由于此方程表示圆，可得5﹣m＞0，解出即可；（2）设M（x1 ， y1），N（x2 ， y2）．与圆的方程联立可得△＞0及根与系数关系，再利用 ， =0，即可解出m．
科目：高中数学 来源： 题型：
【题目】下列关于公差d＞0的等差数列{an}的四个命题：
p1：数列{an}是递增数列；
p2：数列{nan}是递增数列；
p3：数列 
是递增数列；
p4：数列{an+3nd}是递增数列；
其中真命题是（ ）
A.p1 ， p2
B.p3 ， p4
C.p2 ， p3
D.p1 ， p4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知向量 
=（ 
， 
）， 
=（2，cos2x﹣sin2x）．
（1）试判断 与 能否平行？请说明理由．
（2）若x∈（0， 
]，求函数f（x）= 的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知命题p：关于x的不等式x2+2ax+4＞0，对一切x∈R恒成立，q：函数f（x）=（3﹣2a）x是增函数，若p或q为真，p且q为假，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知Sn为数列{an}的前n项和，且an＞0，an2+an=2Sn ．
（1）求数列{an}的通项公式；
（2）令bn= 
，记Tn=b12b32…b2n﹣12 ， 求证：Tn≥ 
．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=3x2+bx+c，不等式f（x）＞0的解集为（﹣∞，﹣2）∪（0，+∞）．
（1）求函数f（x）的解析式；
（2）已知函数g（x）=f（x）+mx﹣2在（2，+∞）上单调递增，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜ 
）离y轴最近的零点与最大值均在抛物线y=﹣ 
x2+ 
x+1上，则f（x）=（ ）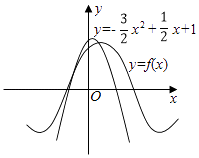
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
