
【题目】已知函数f(x)=x﹣ ![]() .
.
(1)判断函数f(x)的奇偶性,并加以证明;
(2)用定义证明函数f(x)在区间[1,+∞)上为增函数;
(3)若函数f(x)在区间[2,a]上的最大值与最小值之和不小于 ![]() ,求a的取值范围.
,求a的取值范围.
【答案】
(1)解:函数 ![]() 是奇函数.
是奇函数.
∵定义域:(﹣∞,0)∪(0,+∞),定义域关于原点对称,
且 ![]()
∴函数 ![]() 是奇函数
是奇函数
(2)证明:设任意实数x1,x2∈[1,+∞),且x1<x2
则 ![]() ﹣(
﹣( ![]() )═
)═ ![]()
═ ![]() =
= ![]() =
= ![]()
∵x1<x2,x1,x2∈[1,+∞)
∴x1﹣x2<0,x1x2>0,x1x2+1>0,
∴ ![]() <0
<0
∴f(x1)﹣f(x2)<0,即f(x1)<f(x2)
∴函数f(x)在区间[1,+∞)上为增函数
(3)解:∵[2,a][1,+∞)
∴函数f(x)在区间[2,a]上也为增函数.
∴ ![]() ,
, ![]()
若函数f(x)在区间[2,a]上的最大值与最小值之和不小于 ![]() ,
,
则 ![]()
解得a≥4,
∴a的取值范围是[4,+∞)
【解析】(1)判断出函数是奇函数再证明,确定函数定义域且关于原点对称,利用奇函数的定义可判断;(2)判断函数f(x)在(0,+∞)上是增函数,证明按照取值、作差、变形定号、下结论步骤即可;(3)根据(2)的结论得函数在区间[2,a]上的单调性,再求出最大值、最小值,根据条件列出不等式求出a得范围.
【考点精析】关于本题考查的函数奇偶性的性质和利用导数研究函数的单调性,需要了解在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能得出正确答案.
在这个区间单调递减才能得出正确答案.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:
【题目】如图所示,函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )离y轴最近的零点与最大值均在抛物线y=﹣
)离y轴最近的零点与最大值均在抛物线y=﹣ ![]() x2+
x2+ ![]() x+1上,则f(x)=( )
x+1上,则f(x)=( )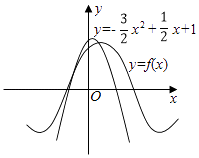
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作,约成书于四、五世纪,也就是大约一千五百年前,传本的《孙子算经》共三卷,卷中有一问题:“今有方物一束,外周一匝有三十二枚,问积几何?”该著作中提出了一种解决问题的方法:“重置二位,左位减八,余加右位,至尽虚加一,即得.”通过对该题的研究发现,若一束方物外周一匝的枚数![]() 是8的整数倍时,均可采用此方法求解,如图,是解决这类问题的程序框图,若输入
是8的整数倍时,均可采用此方法求解,如图,是解决这类问题的程序框图,若输入![]() ,则输出的结果为( )
,则输出的结果为( )
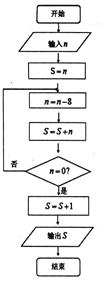
A. 120 B. 121 C. 112 D. 113
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点. 
(1)证明:面PAD⊥面PCD;
(2)求直线AC与PB所成角的余弦值;
(3)求二面角A﹣MC﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)对任意实数x,y满足f(x)+f(y)=f(x+y)+3,f(3)=6,当x>0 时,f(x)>3,那么,当f(2a+1)<5时,实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() ﹣
﹣ ![]() ,则使得f(2x)>f(x﹣3)成立的x的取值范围是( )
,则使得f(2x)>f(x﹣3)成立的x的取值范围是( )
A.(﹣∞,﹣3)
B.(1,+∞)
C.(﹣3,﹣1)
D.(﹣∞,﹣3)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,曲线
,曲线![]() 上任意一点
上任意一点![]() 满足
满足![]() ;曲线
;曲线![]() 上的点
上的点![]() 在
在![]() 轴的右边且
轴的右边且![]() 到
到![]() 的距离与它到
的距离与它到![]() 轴的距离的差为1.
轴的距离的差为1.
(1)求![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与
与![]() 相交于点
相交于点![]() ,直线
,直线![]() 分别与
分别与![]() 相交于点
相交于点![]() 和
和![]() .求
.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com