
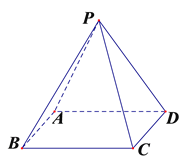
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点. 
(1)证明:面PAD⊥面PCD;
(2)求直线AC与PB所成角的余弦值;
(3)求二面角A﹣MC﹣B的余弦值.
【答案】
(1)证明:∵四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,
∴AD⊥DC,
∵PA⊥底面ABCD,CD平面ABCD,
∴PD⊥DC,
∵PD∩AD=D,
∴CD⊥平面PAD,
∵CD平面PCD,∴面PAD⊥面PCD.
(2)解:∵四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,
PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点,
∴以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,
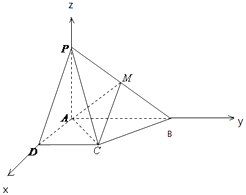
则A(0,0,0),C(1,1,0),P(0,0,1),B(0,2,0),
![]() =(1,1,0),
=(1,1,0), ![]() =(0,2,﹣1),
=(0,2,﹣1),
设直线AC与PB所成角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴直线AC与PB所成角的余弦值为 ![]() .
.
(3)解:A(0,0,0),M(0,1, ![]() ),C(1,1,0),B(0,2,0),
),C(1,1,0),B(0,2,0),
![]() =(1,1,0),
=(1,1,0), ![]() =(0,1,
=(0,1, ![]() ),
), ![]() =(1,﹣1,0),
=(1,﹣1,0), ![]() =(0,﹣1,
=(0,﹣1, ![]() ),
),
设平面ACM的法向量 ![]() =(x,y,z),
=(x,y,z),
则 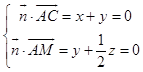 ,取x=1,得
,取x=1,得 ![]() =(1,﹣1,2),
=(1,﹣1,2),
设平面BCM的法向量 ![]() =(a,b,c),
=(a,b,c),
则 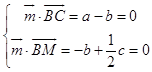 ,取a=1,得
,取a=1,得 ![]() =(1,1,2),
=(1,1,2),
设二面角A﹣MC﹣B的平面角为α,
则cosα= ![]() =
= ![]() =
= ![]() .
.
∵二面角A﹣MC﹣B是钝二面角,
∴二面角A﹣MC﹣B的余弦值为﹣ ![]() .
.
【解析】(1)推导出AD⊥DC,PD⊥DC,从而CD⊥平面PAD,由此能证明面PAD⊥面PCD.(2)以A为原点,AD为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出直线AC与PB所成角的余弦值.(3)求出平面ACM的法向量和平面BCM的法向量,利用向量法能求出二面角A﹣MC﹣B的余弦值.
【考点精析】本题主要考查了异面直线及其所成的角和平面与平面垂直的判定的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象向左平移 ![]() 个单位,得到的图象对应的解析式是( )
个单位,得到的图象对应的解析式是( )
A.y=sin(2x+ ![]() )
)
B.y=sin( ![]() x+
x+ ![]() )
)
C.y=sin( ![]() x+
x+ ![]() )
)
D.y=sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(sinx+cosx)2+2cos2x﹣2.
(1)求函数f(x)的最小正周期及单调递增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是根据某班50名同学在某次数学测验中的成绩(百分制)绘制的概率分布直方图,其中成绩分组区间为:[40,50),[50,60),…,[80,90),[90,100]. 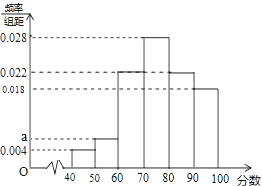
(1)求图中a的值;
(2)计算该班本次的数学测验成绩不低于80分的学生的人数;
(3)根据频率分布直方图,估计该班本次数学测验成绩的平均数与中位数(要求中位数的估计值精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x+1)的定义域是[﹣1,3],则y=f(x2)的定义域是( )
A.[0,4]
B.[0,16]
C.[﹣2,2]
D.[1,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() .
.
(1)判断函数f(x)的奇偶性,并加以证明;
(2)用定义证明函数f(x)在区间[1,+∞)上为增函数;
(3)若函数f(x)在区间[2,a]上的最大值与最小值之和不小于 ![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD![]() 底面ABCD,
底面ABCD, ![]() ;
;
(1)求证:平面PAB![]() 平面PCD;
平面PCD;
(2)若过点B的直线![]() 垂直平面PCD,求证:
垂直平面PCD,求证: ![]() //平面PAD.
//平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣4|x|+3,x∈R.
(1)判断函数的奇偶性并将函数写成分段函数的形式;
(2)画出函数的图象,根据图象写出它的单调区间; 
(3)若函数f(x)的图象与y=a的图象有四个不同交点,则实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com