
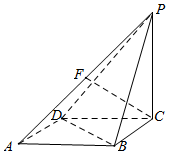
 在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PA的中点.
在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PA的中点.分析 (Ⅰ)连接AC,交BD于点O,连接PO,则PO与CF相交,设交点为E,则AC⊥BD,PC⊥BD,BD⊥CF,PO⊥CF,由此能证明CF⊥平面PDB.
(Ⅱ)过点P作PG,使得 PG=BC,则GP∥AD∥BC,从而二面角AD-P-BC,即二面角C-PG-D,在平行四边形ADGP中,过点P作AD的垂线,垂足为H,则∠HPC即所求二面角的平面角,由此能求出平面ADP与平面BCP所成锐二面角的余弦值.
解答 证明:(Ⅰ)连接AC,交BD于点O,连接PO,由于PO,CF?平面PAC,
所以PO与CF相交,设交点为E,
∵底面ABCD为菱形,∴AC⊥BD,又∵PC⊥平面ABCD,∴PC⊥BD,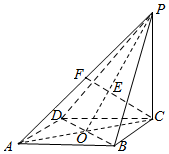
∴BD⊥平面PAC,又∵CF?平面PAC,∴BD⊥CF,
在△PAC中,∵∠DAB=60°,AB=2,∴AC=2$\sqrt{3}$,OC=$\sqrt{3}$,
CF=PF=$\frac{3\sqrt{2}}{2}$,PO=3,
∴cos∠FCP=$\frac{(\frac{3\sqrt{2}}{2})^{2}+(\sqrt{6})^{2}-(\frac{3\sqrt{2}}{2})^{2}}{2×\frac{3\sqrt{2}}{2}×\sqrt{6}}$=$\frac{\sqrt{3}}{3}$,sin∠OPC=$\frac{\sqrt{3}}{3}$,
∴cos∠FCP=sin∠OPC,又∵两个角都是锐角,
∴∠FCP+∠OPC=90°,则∠PEC=90°,即PO⊥CF,
∵PO∩BD=E,PO、BD?平面PAC,∴CF⊥平面PDB,
解:(Ⅱ)过点P作PG,使得 PG=BC,则底面ABCD为菱形,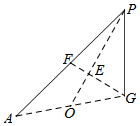 ∴GP∥AD∥BC,∴二面角AD-P-BC,即二面角C-PG-D
∴GP∥AD∥BC,∴二面角AD-P-BC,即二面角C-PG-D
在平行四边形ADGP中,过点P作AD的垂线,垂足为H,则PH⊥PG
又∵PC⊥平面ABCD∴PC⊥BC∴PC⊥PG
∴∠HPC即所求二面角的平面角
∵AD⊥PH,AD⊥PC,∴AD⊥平面HPC,∴AD⊥CH,
又∵∠HDC=60°,DC=2,∴$HC=CD•sin{60°}=2•\frac{{\sqrt{3}}}{2}=\sqrt{3}$,
在△HPC中,∠PCH=90°,$PC=\sqrt{6}$,$HC=\sqrt{3}$,∴PH=3,
∴$cos∠HPC=\frac{PC}{PH}=\frac{{\sqrt{6}}}{3}$,即所求二面角的平面角的余弦值为$\frac{{\sqrt{6}}}{3}$.
点评 本题考查线面垂直的证明,考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
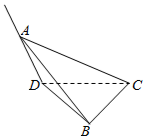 如图,在二面角A-CD-B中,BC⊥CD,BC=CD=2,点A在直线AD上运动,满足AD⊥CD,AB=3.现将平面ADC沿着CD进行翻折,在翻折的过程中,线段AD长的取值范围是$[\sqrt{5}-2,\sqrt{5}+2]$.
如图,在二面角A-CD-B中,BC⊥CD,BC=CD=2,点A在直线AD上运动,满足AD⊥CD,AB=3.现将平面ADC沿着CD进行翻折,在翻折的过程中,线段AD长的取值范围是$[\sqrt{5}-2,\sqrt{5}+2]$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab>ac | B. | c(b-a)>0 | C. | ac(a-c)<0 | D. | cb2>ab2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com