
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
分析 由题意可求得函数是一个周期函数,且周期为2,故可以研究出一个周期上的函数图象,再研究所给的区间包含了几个周期即可知道在这个区间中的零点的个数.
解答 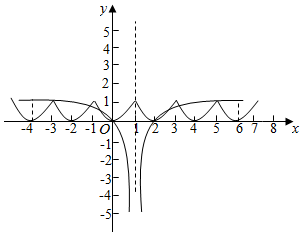 解:函数f(x)是R上的偶函数,f(x+2)=f(x),即函数的周期是2
解:函数f(x)是R上的偶函数,f(x+2)=f(x),即函数的周期是2
又x∈[0,1]时,f(x)=x2,要研究函数y=f(x)-log5|x-1|零点个数,
可将问题转化为y=f(x)与y=log5|x-1|有几个交点,
如图
由图知,有10个交点
故选:C.
点评 本题考查函数的零点,求解本题,关键是研究出函数f(x)性质,作出其图象,将函数y=f(x)-log5|x-1|的零点个数的问题转化为两个函数交点个数问题是本题中的一个亮点,此一转化使得本题的求解变得较容易.


科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 1 | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
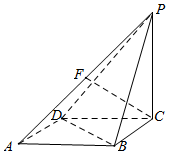 在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PA的中点.
在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{39}}}{39}$ | B. | $\frac{{\sqrt{13}}}{13}$ | C. | $\frac{{\sqrt{13}}}{39}$ | D. | $\frac{{\sqrt{39}}}{13}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com