
分析 (Ⅰ)通过讨论x的范围求出不等式的解集即可;(Ⅱ)根据直线的垂直关系,求出关于a,b的等式,根据基本不等式的性质证明即可.
解答 解:(Ⅰ)设f(x)=|2x-4|+|x+1|,
∵f(x)=$\left\{\begin{array}{l}{3x-3,x≥2}\\{-x+5,-1≤x<2}\\{-3x+3,x<-1}\end{array}\right.$,
x≥2时,3x-3≥5,解得:x≥$\frac{8}{3}$,
-1≤x<2时,-x+5≥5,解得:x≤0,
x<-1时,-3x+3≥5,解得:x≤-$\frac{2}{3}$,
综上,不等式的解集是(-∞,0]∪[$\frac{8}{3}$,+∞).
(Ⅱ)证明:∵直线(a-1)x+2y+6=0与直线2x+by-5=0互相垂直,
∴2(a-1)+2b=0,得:a+b=1,
∵ab≤${(\frac{a+b}{2})}^{2}$=$\frac{1}{4}$,当且仅当a=b时取“=”,
∴$\frac{1}{ab}$≥4,
∴$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$≥$\frac{2}{ab}$≥8,当且仅当a=b=$\frac{1}{2}$时取“=”,
即:$\frac{1}{{a}^{2}}+\frac{1}{{b}^{2}}$≥8.
点评 本题考查了解绝对值不等式问题,考查基本不等式的性质,是一道中档题.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3x+4y-20=0 | B. | 4x+3y-4=0 | C. | 3x-4y-15=0 | D. | 4x-3y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
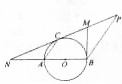 如图,AB是⊙O的直径,C是⊙O上一点,AC∥BP,BM切⊙O于B,BM交CP于M,且CM=MP.
如图,AB是⊙O的直径,C是⊙O上一点,AC∥BP,BM切⊙O于B,BM交CP于M,且CM=MP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
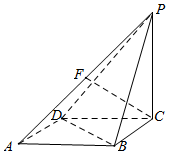 在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PA的中点.
在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com