
【题目】双曲线C的方程为![]() 离心率
离心率![]() 顶点到渐近线的距离为
顶点到渐近线的距离为![]()
(1)求双曲线C的方程;
(2)点P是双曲线C上一点,A,B两点在双曲线C的两条渐近线上,且分别位于第一,二象限.若![]() 求△AOB面积的取值范围。
求△AOB面积的取值范围。
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)先由双曲线标准方程求得顶点坐标和渐近线方程,进而根据顶点到渐近线的距离求得a,b和c的关系,进而根据离心率求得a和c的关系,最后根据c=![]() 综合得方程组求得a,b和c,则双曲线方程可得.(Ⅱ)由(Ⅰ)可求得渐近线方程,设A(m,2m),B(-n,2n),根据
综合得方程组求得a,b和c,则双曲线方程可得.(Ⅱ)由(Ⅰ)可求得渐近线方程,设A(m,2m),B(-n,2n),根据![]() 得P点的坐标代入双曲线方程化简整理m,n与λ的关系式,设∠AOB=2θ,进而根据直线的斜率求得tanθ,进而求得sin2θ,进而表示出|OA|,得到△AOB的面积的表达式,根据λ的范围求得三角形面积的最大值和最小值,△AOB面积的取值范围可得
得P点的坐标代入双曲线方程化简整理m,n与λ的关系式,设∠AOB=2θ,进而根据直线的斜率求得tanθ,进而求得sin2θ,进而表示出|OA|,得到△AOB的面积的表达式,根据λ的范围求得三角形面积的最大值和最小值,△AOB面积的取值范围可得
试题解析:(Ⅰ)由题意知,双曲线C的顶点![]() 到渐近线
到渐近线![]()
∴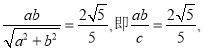 [由
[由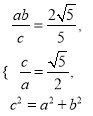 得
得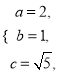 ∴双曲线C的方程为
∴双曲线C的方程为![]()
(Ⅱ)设直线AB的方程为![]() 由题意知
由题意知![]() 由{
由{![]()
得A点的坐标为![]() 由{
由{![]() 得B点的坐标为
得B点的坐标为![]()
由![]() 得P点的坐标为
得P点的坐标为![]()
将P点坐标代入![]() 设Q为直线AB与y轴的交点,则Q点的坐标为(0,m).
设Q为直线AB与y轴的交点,则Q点的坐标为(0,m).
![]() =
=![]()
设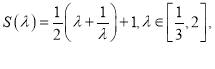 在
在![]() 上是减函数,在
上是减函数,在![]() 上是减函数
上是减函数
当![]() 时,△AOB的面积取得最小值2,当
时,△AOB的面积取得最小值2,当![]() 时,△AOB的面积取得最大值
时,△AOB的面积取得最大值![]()
∴△AOB面积的取值范围是![]()


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:高中数学 来源: 题型:
【题目】已知a、b、c是互不相等的非零实数.若用反证法证明三个方程ax2+2bx+c=0,bx2+2cx+a=0,cx2+2ax+b=0至少有一个方程有两个相异实根,应假设成( )
A. 三个方程都没有两个相异实根 B. 一个方程没有两个相异实根
C. 至多两个方程没有两个相异实根 D. 三个方程不都没有两个相异实根
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,E、F分别是A1B、A1C的中点,点D在B1C1上,A1D⊥B1C.

求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用反证法证明“自然数a,b,c中恰有一个偶数”时,下列假设正确的是 ( )
A.假设a,b,c都是奇数或至少有两个偶数
B.假设a,b,c都是偶数
C.假设a,b,c至少有两个偶数
D.假设a, b,c都是奇数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).若直线
为参数).若直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .
.
(Ⅰ)写出圆![]() 的直角坐标方程,并求圆心的坐标与半径;
的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com