
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(理)试卷(解析版) 题型:解答题
设函数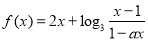 为奇函数,
为奇函数,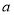 为常数.
为常数.
(Ⅰ)求实数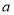 的值;
的值;
(Ⅱ)求函数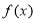 的单调区间;
的单调区间;
(Ⅲ)若对于区间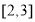 上的每一个
上的每一个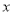 值,不等式
值,不等式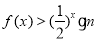 恒成立,求实数
恒成立,求实数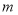 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(文)试卷(解析版) 题型:解答题
已知函数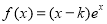 (
(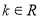 ).
).
(1)求 的单调区间和极值;
的单调区间和极值;
(2)求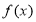 在
在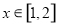 上的最小值.
上的最小值.
(3)设 ,若对
,若对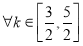 及
及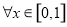 有
有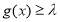 恒成立,求实数
恒成立,求实数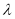 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>c>b | B. | b>a>c | C. | c>b>a | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [m2,2m2] | B. | [2m2,3m2] | C. | [3m2,4m2] | D. | [4m2,5m2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com