
已知函数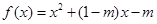
(1)若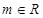 ,解不等式
,解不等式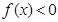 ;
;
(2)若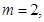 解不等式
解不等式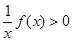
(1)当 时,不等式的解集为:
时,不等式的解集为:
 时,不等式的解集为:
时,不等式的解集为:
 时,不等式的解集为:空集 ;
时,不等式的解集为:空集 ;
(2) {x| 或
或 }。
}。
解析试题分析: (1)根据已知不等式进行因式分解,然后得到方程的根,结合判别式得到不同的解集。
(2)当m=2时,则不等式化为: ,将分式化为整式来计算得到。
,将分式化为整式来计算得到。
解:(1)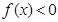 即为
即为
当 时,不等式的解集为:
时,不等式的解集为:
 时,不等式的解集为:
时,不等式的解集为:
 时,不等式的解集为:空集 -----------------------------6分
时,不等式的解集为:空集 -----------------------------6分
(2)当 时,不等式化为:
时,不等式化为: 即为:
即为:
 原不等式的解集为:
原不等式的解集为: 或
或 ----------------------12分
----------------------12分
考点:本题主要考查了一元二次不等式的求解以及函数参数分类讨论思想的运用。
点评:解决该试题的关键是对于m为实数,结合一元二次不等式的求解方法,进行确定出m的三种情况,分类讨论得到。


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源:2014届四川省高二10月月考理科数学试卷(解析版) 题型:解答题
已知函数
(1)若不等式 的解集为
的解集为 求实数
求实数 的值
的值
(2)在(1)的条件下 若
若 对一切实数
对一切实数 恒成立
恒成立 求实数
求实数 的
的
取值范围
查看答案和解析>>
科目:高中数学 来源:2012-2013学年辽宁省高三入学摸底考试理科数学试卷(解析版) 题型:解答题
(本小题10分)选修4—5:不等式选讲
已知函数
(1)若不等式 的解集为
的解集为 ,求实数
,求实数 的值;
的值;
(2)当 时,解关于
时,解关于 的不等式
的不等式 .
.
查看答案和解析>>
科目:高中数学 来源:2014届湖北省高一上学期期末考试理科数学 题型:解答题
. (14分)已知函数
(1)若使函数 在
在 上为减函数,求
上为减函数,求 的取值范围;
的取值范围;
(2)当 =
= 时,求
时,求 的值域;
的值域;
(3)若关于 的方程
的方程 在
在 上仅有一解,求实数
上仅有一解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一第二次月考数学试卷 题型:解答题
已知函数
(1)若使函数f(x)在 上为减函数,求a的取值范围;
上为减函数,求a的取值范围;
(2)当a = 时,求y= f(
时,求y= f( ),
),  的值域.
的值域.
(3)若关于x的方程f(x)=-1+  在[1,3]上有且只有一解,求a的取值范围.
在[1,3]上有且只有一解,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com