
分析 根据抽象函数的关系,利用赋值法将不等式进行转化,结合函数的单调性进行求解即可.
解答 解:∵f(x+y)=f(x)f(y),f(1)=3,
∴f(1+1)=f(1)f(1)=3×3=9,
即f(2)=9,
则f(3)=f(1+2)f(1)f(2)=3×9=27,
则不等式,f(x)f(x2-3)≤27等价为f(x+x2-3)≤f(3),
∵f(x)是定义在(0,+∞)上的增函数,
∴$\left\{\begin{array}{l}{x>0}\\{{x}^{2}-3>0}\\{{x}^{2}+x-3≤3}\end{array}\right.$,即$\left\{\begin{array}{l}{x>0}\\{x>\sqrt{3}或x<-\sqrt{3}}\\{-3≤x≤2}\end{array}\right.$,
即$\sqrt{3}$<x≤2,
即不等式的解集为:($\sqrt{3}$,2],
故答案为:($\sqrt{3}$,2]
点评 本题主要考查不等式的求解,利用抽象函数的定义关系,利用赋值法将不等式进行转化是解决本题的关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{5}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
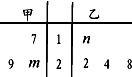 已知甲、乙两组数据如图茎叶图所示,若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )
已知甲、乙两组数据如图茎叶图所示,若它们的中位数相同,平均数也相同,则图中的m,n的比值$\frac{m}{n}$=( )| A. | $\frac{3}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,-$\sqrt{2}$) | B. | (1,-1) | C. | (1,-i) | D. | (2,-2i) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com