
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
分析 (Ⅰ)求出样本中心点的坐标,可得${\;}_{a}^{∧}$,即可回归直线方程$\widehat{y}$=$\widehat{b}$x+$\hat{a}$;
(Ⅱ)确定利润函数,利用配方法,即可得出结论.
解答 解:(Ⅰ)由题意,$\overline{x}=8.5,\overline{y}=80,\hat{y}=-20x+250$;
(Ⅱ)$L=(x-5)(-20x+250)=-20{{(x-\frac{35}{4})}^{2}}+281.25$,
所以当x=8.75时,工厂获得最大利润.
点评 本题考查回归直线方程,考查利用数学知识解决实际问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
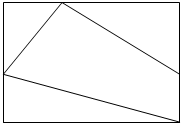 用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )
用5种不同的颜色给图中四个区域涂色,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,不同的涂色方法有( )| A. | 180 | B. | 240 | C. | 160 | D. | 320 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{2}$+3 | B. | $-2\sqrt{2}-3$ | C. | $2\sqrt{2}+3$ | D. | $2\sqrt{2}-3$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -1 | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com