
分析 a1=3,an+1=3nan,可得n≥2时,$\frac{{a}_{n}}{{a}_{n-1}}$=3n-1,利用“累乘求积”方法即可得出.
解答 解:∵a1=3,an+1=3nan,
∴n≥2时,$\frac{{a}_{n}}{{a}_{n-1}}$=3n-1,
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{3}}{{a}_{2}}$•$\frac{{a}_{2}}{{a}_{1}}$•a1
=3n-1×3n-2×…×32×3×1
=${3}^{\frac{(n-1)n}{2}}$,
n=1时也成立.
∴an=${3}^{\frac{(n-1)n}{2}}$,
故答案为:${3}^{\frac{(n-1)n}{2}}$.
点评 本题考查了“累乘求积”方法、等差数列的求和公式、指数运算性质,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
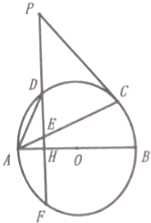 已知AC是以AB为直径的⊙O的一条弦,点D是劣弧$\widehat{AC}$上的一点,过点D作DH⊥AB于H,交AC于E,延长线交⊙O于F.
已知AC是以AB为直径的⊙O的一条弦,点D是劣弧$\widehat{AC}$上的一点,过点D作DH⊥AB于H,交AC于E,延长线交⊙O于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,-$\sqrt{2}$) | B. | (1,-1) | C. | (1,-i) | D. | (2,-2i) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com