
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() ,求实数
,求实数![]() 取值的集合;
取值的集合;
(Ⅱ)当![]() 时,对任意
时,对任意![]() ,
,![]() ,令
,令![]() ,证明
,证明![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(I)f′(x)![]() .(x>0).对a分类讨论即可得出单调性极值与最值.进而得出a的取值集合;(II)当a=0时,f(x)=lnx,则
.(x>0).对a分类讨论即可得出单调性极值与最值.进而得出a的取值集合;(II)当a=0时,f(x)=lnx,则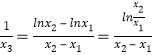 ,由(I)可知:lnx
,由(I)可知:lnx![]() 1≥0,(x>0).根据0<x1<x2,可得
1≥0,(x>0).根据0<x1<x2,可得![]() 1,ln
1,ln![]() 1
1![]() ,即可证明
,即可证明![]() .由(I)可知:lnx<x﹣1,(x>1).同理可证明:
.由(I)可知:lnx<x﹣1,(x>1).同理可证明:![]() .
.
(Ⅰ)由已知,有![]() .
.
当![]() 时,
时,![]() ,与条件
,与条件![]() 矛盾;
矛盾;
当![]() 时,若
时,若![]() ,则
,则![]() ,
,![]() 单调递减;
单调递减;
若![]() ,则
,则![]() ,
,![]() 单调递增.
单调递增.
∴![]() 在
在![]() 上有最小值
上有最小值![]() .
.
由题意![]() ,∴
,∴![]() .
.
令![]() .∴
.∴![]() .
.
当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
∴![]() 在
在![]() 上有最大值
上有最大值![]() .∴
.∴![]() .
.
∴![]() .
.
∴![]() ,∴
,∴![]() ,
,
综上,当![]() 时,实数
时,实数![]() 取值的集合为
取值的集合为![]() .
.
(Ⅱ)当![]() 时,
时,![]() ,则
,则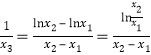 .
.
由(Ⅰ),可知![]() .
.
∴![]() (当且仅当
(当且仅当![]() 时取等号). ①
时取等号). ①
∵![]() ,∴
,∴![]() .∴
.∴![]() ,∴
,∴![]()
由①式可得当![]() 时,有
时,有![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.
综上所述,有![]() ,∴
,∴![]() .
.


科目:高中数学 来源: 题型:
【题目】已知双曲线C和椭圆![]() 1有公共的焦点,且离心率为
1有公共的焦点,且离心率为![]() .
.
(1)求双曲线C的方程;
(2)经过点M(2,1)作直线l交双曲线C于A、B两点,且M为AB的中点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() =2px经过点
=2px经过点![]() (1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(1,2).过点Q(0,1)的直线l与抛物线C有两个不同的交点A,B,且直线PA交y轴于M,直线PB交y轴于N.
(Ⅰ)求直线l的斜率的取值范围;
(Ⅱ)设O为原点,![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论正确是( )
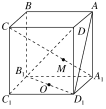
A.A,M,O三点共线B.A,M,O,A1不共面
C.A,M,C,O不共面D.B,B1,O,M共面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络平台从购买该平台某课程的客户中,随机抽取了100位客户的数据,并将这100个数据按学时数,客户性别等进行统计,整理得到如表:
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根据上表估计男性客户购买该课程学时数的平均值(同一组中的数据用该组区间的中点值作代表,结果保留小数点后两位);
(2)从这100位客户中,对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人,再从这7人中随机抽取2人,求这2人购买的学时数都不低于15的概率.
(3)将购买该课程达到25学时及以上者视为“十分爱好该课程者”,25学时以下者视,为“非十分爱好该课程者”.请根据已知条件完成以下![]() 列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小区打算将如图的一直三角形![]() 区域进行改建,在三边上各选一点连成等边三角形
区域进行改建,在三边上各选一点连成等边三角形![]() ,在其内建造文化景观.已知
,在其内建造文化景观.已知![]() ,
,![]() ,则
,则![]() 区域内面积(单位:
区域内面积(单位:![]() )的最小值为( )
)的最小值为( )
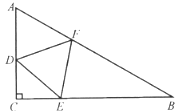
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题
①已知![]() 为椭圆
为椭圆![]() 上任意一点,
上任意一点,![]() ,
,![]() 是椭圆的两个焦点,则
是椭圆的两个焦点,则![]() 的周长是8;
的周长是8;
②已知![]() 是双曲线
是双曲线![]() 上任意一点,
上任意一点,![]() 是双曲线的右焦点,则
是双曲线的右焦点,则![]() ;
;
③已知直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,且
,且![]() 与
与![]() 交于
交于![]() ,
,![]() ,
,![]() ,
,![]() 两点,则
两点,则![]() ;
;
④椭圆具有这样的光学性质:从椭圆的一个焦点出发的光线,经椭圆反射后,反射光线经过椭圆的另一个焦点,今有一个水平放置的椭圆形台球盘,点![]() ,
,![]() 是它的焦点,长轴长为
是它的焦点,长轴长为![]() ,焦距为
,焦距为![]() ,若静放在点
,若静放在点![]() 的小球(小球的半径忽略不计)从点
的小球(小球的半径忽略不计)从点![]() 沿直线出发则经椭圆壁反射后第一次回到点
沿直线出发则经椭圆壁反射后第一次回到点![]() 时,小球经过的路程恰好是
时,小球经过的路程恰好是![]() .
.
其中正确命题的序号为__(请将所有正确命题的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com