
分析 根据题意,由等比数列{an}的a1与q的值,可得其通项公式,又由an=$\frac{1}{3}$,则有$\frac{27}{16}$×(-$\frac{2}{3}$)n-1=$\frac{1}{3}$,解可得n的值,即可得答案.
解答 解:根据题意,等比数列{an}中a1=$\frac{27}{16}$,q=-$\frac{2}{3}$,
则通项公式为an=a1×qn-1=$\frac{27}{16}$×(-$\frac{2}{3}$)n-1,
若an=$\frac{1}{3}$,则有$\frac{27}{16}$×(-$\frac{2}{3}$)n-1=$\frac{1}{3}$,
解可得n=5;
故答案为:5.
点评 本题考查等比数列的通项,注意牢记公式的形式.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ksin(π+α)>0 | B. | kcos(π-α)>0 | C. | ksinα≤0 | D. | kcosα≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
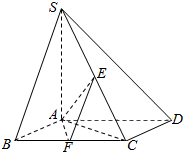 如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.
如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2=2 | B. | 9<x3•x4<25 | C. | 0<(6-x3)•(6-x4)<1 | D. | 1<x1•x2<9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com