分析:(1)在平面ABCD内过点B作AC的平行线BE,由AC∥A1C1,AC∥BE,知BE∥A1C1,故直线BE就是所求的直线l.且l∥A1C1.
(2)由A1C1⊥面DBB1D1,知A1C1⊥B1D.由A1B⊥面ADC1B1,知A1B⊥B1D,所以B1D⊥面A1BC1.
(3)AC∥A1C1,且AC在面A1BC1外,A1C1?面A1BC1,所以AC∥面A1BC1,直线AC到面A1BC1的距离即为点A到面A1BC1的距离,记为h,由等积法能求出线AC到面A1BC1的距离.
解答:(1)解:在平面ABCD内过点B作AC的平行线BE,
∵AC∥A
1C
1,AC∥BE,
∴BE∥A
1C
1,
∴面A
1BC
1与面ABCD的交线l与BE重合,
即直线BE就是所求的直线l.
∵BE∥A
1C
1,
l与BE重合,
∴l∥A
1C
1.
(2)证明:连接B
1D
1,
∵A
1B
1C
1D
1是正方形,
∴A
1C
1⊥B
1D
1,
∵A
1C
1⊥DD
1,
∴A
1C
1⊥面DBB
1D
1,
∴A
1C
1⊥B
1D.
同理A
1B⊥面ADC
1B
1,
∴A
1B⊥B
1D,
∵A
1C
1∩A
1B=A
1,
∴B
1D⊥面A
1BC
1.
(3)解:∵AC∥A
1C
1,且AC在面A
1BC
1外,A
1C
1?面A
1BC
1,
∴AC∥面A
1BC
1,
∴直线AC到面A
1BC
1的距离即为点A到面A
1BC
1的距离,记为h,
在三棱锥中A-A
1BC
1中,
VA_A1BC1=VC1-ABA1,
∵正方体A
1B
1C
1D
1-ABCD棱长为a,
∴
VA-A1BC1=
•
S△A1B C1•h=
××(a)2×h×sin60°=
h,
VC1-ABA1=
•S△ABA1•A
1C
1=
××a×a×a=
,
∵
VA-A1BC1=
VC1-ABA1,
∴h=
a.
点评:本题考查空间中点、线、面间的距离,证明直线和平面垂直,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,易出错.解题时要认真审题,仔细解答.

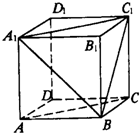 如图,在棱长为a的正方体A1B1C1D1-ABCD中,
如图,在棱长为a的正方体A1B1C1D1-ABCD中,

 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案![]() ,AG=
,AG=![]() ,给出下列四个命题:①AC⊥BD,②FG=
,给出下列四个命题:①AC⊥BD,②FG=![]() ,③侧面与底面所成二面角的余弦值为
,③侧面与底面所成二面角的余弦值为![]() ,④
,④![]() ,其中真命题的序号是( )
,其中真命题的序号是( )




