
|
|
| a+m |
| b+m |
| a |
| b |
| 4 |
| x |
| 3 |
| 1 |
| d |
| 1 |
| c |
| a |
| d |
| b |
| c |
|
|
| a+m |
| b+m |
| a |
| b |
| m(b-a) |
| b(b+m) |
| a+m |
| b+m |
| a |
| b |
| 4 |
| x |
| 3 |
| 4 |
| x |
| 3 |


科目:高中数学 来源:2014届黑龙江省高二上学期期末理科数学试卷(解析版) 题型:选择题
下列命题中真命题的是( )
A.在同一平面内,动点到两定点的距离之差(大于两定点间的距离)为常数的点的轨迹是双曲线
B.在平面内,F1,F2是定点,|F1F2|=6,动点M满足|MF1|+|MF2|=6,则点M的轨迹是椭圆
C.“若-3<m<5则方程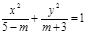 是椭圆”
是椭圆”
D.在直角坐标平面内,到点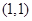 和直线
和直线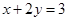 距离相等的点的轨迹是直线
距离相等的点的轨迹是直线
查看答案和解析>>
科目:高中数学 来源:2011-2012学年高二(上)期末数学试卷(文科)(解析版) 题型:选择题
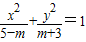 是椭圆”
是椭圆”查看答案和解析>>
科目:高中数学 来源: 题型:
①若在一个平面内有无数个点到另一个平面的距离相等,则这两个平面平行 ②若两个平面和一条直线都不垂直,则这两个平面不平行 ③若直线a、b是异面直线,a![]() 平面α,则过b没有和α平行的平面
平面α,则过b没有和α平行的平面
A.0 B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com