练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    求通过直线l:2x+y+4=0及圆C:x2+y2+2x-4y+1=0的交点，并且有最小面积的圆的方程.

    解析：解法一:圆的方程为(x+1)2+(y-2)2=4.设直线l与圆C交于A、B两点，D为AB的中点，则直线CD的方程为x-2y+5=0,x-2y+5=0,2x+y+4=0.故D

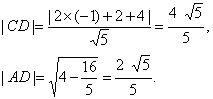
    ∴以D为圆心，AB为直径的圆是面积最小的圆.?

    解法二:设圆的方程是(x2+y2+2x-4y+1)+λ(2x+y+4)=0,即［x+(1+λ)2］+

    圆面积=πR2,?

    而时，圆面积最小，此时圆的方程是5x2+5y2+26x-12y+37=0.?

    解法三:设A(x1,y1),B(x2,y2),则以AB为直径的圆方程可设为(x-x1)(x-x2)+(y-y1)(y-y2)=0,?

    即x2+y2-(x1+x2)x-(y1+y2)y+x1x2+y1y2=0.然后用韦达定理求出圆的方程.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高考总复习全解　数学　一轮复习·必修课程　（人教实验版）　B版 人教实验版　B版 题型：044

    求满足下列条件的直线方程：

    (1)求通过点(－2，2)，且与两坐标轴所围成的三角形面积为1的直线l的方程；

    (2)已知直线l1：2x＋y－6＝0和点A(1，－1)，过点A作直线l与已知直线相交于B点，且|AB|＝5，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源：设计必修二数学北师版 北师版 题型：044

    求通过直线l：2x＋y＋4＝0及圆C：x2＋y2＋2x－4y＋1＝0的交点，并且有最小面积的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源：设计必修二数学人教A版 人教A版 题型：044

    求通过直线l：2x＋y＋4＝0及圆C：x2＋y2＋2x－4y＋1＝0的交点，并且有最小面积的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求通过直线l:2x+y+4=0及圆C:x2+y2+2x-4y+1=0的交点,并且有最小面积的圆的方程.

    查看答案和解析>>

    同步练习册答案