如图.直线l与抛物线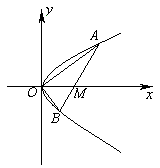交于两点.与x轴相交于点M.且． (1)求证:M点的坐标为(1.0), (2)求证:OA⊥OB, (3)求△AOB的面积的最小值．题目和参考答案——青夏教育精英家教网—

如图，直线l与抛物线交于两点，与x轴相交于点M，且．

(1)求证：M点的坐标为(1，0)；

(2)求证：OA⊥OB；

(3)求△AOB的面积的最小值．

答案：
解析：

答案：(3)1

(1 ) 设M点的坐标为(x₀，0)，直线l方程为 x =my + x₀ ，代入y²=x得

y²－my－x₀=0　　　　①　　y₁、y₂是此方程的两根，

∴ x₀ ＝－y₁y₂ ＝1，即M点的坐标为(1，0)．

(2 ) ∵ y₁y₂ ＝－1

∴ x₁x₂ + y₁y₂ =y₁²y₂² +y₁y₂ ＝y₁y₂(y₁y₂ +1) =0

∴　OA⊥OB．

(3)由方程①，y₁＋y₂ =m ，　y₁y₂ ＝－1 ，　且 | OM | =x₀=1，

于是S_△AOB=| OM | |y₁－y₂| ==≥1，

∴ 当m =0时，△AOB的面积取最小值1．

练习册系列答案

书立方期末大考卷系列答案

相关习题

科目：高中数学 来源： 题型：

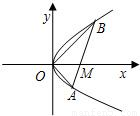
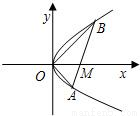
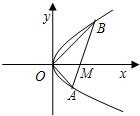如图，直线l与抛物线y²=x交于A（x₁，y₁），B（x₂，y₂）两点，与x轴相交于点M，且y₁y₂=-1．
（1）求证：M点的坐标为（1，0）；
（2）求证：OA⊥OB；
（3）求△AOB的面积的最小值．

科目：高中数学 来源：0103 月考题 题型：解答题

如图，直线l与抛物线y²=x交于A（x₁，y₁），B（x₂，y₂）两点，与x轴相交于点M，且y₁y₂=-1，
（1）求证：M点的坐标为（1，0）；
（2）求证：OA⊥OB；
（3）求△AOB的面积的最小值。

科目：高中数学 来源：不详 题型：解答题

科目：高中数学 来源：2012-2013学年河南省驻马店市泌阳一高高二（上）12月月考数学试卷（文科）（解析版） 题型：解答题

科目：高中数学 来源：2011年高三数学单元检测：圆锥曲线与方程（2）（解析版） 题型：解答题

同步练习册答案