Question

等轴双曲线x²-y²=a²与直线y=ax（a＞0）没有公共点，则a的取值范围（ ）
A．a=1
B．0＜a＜1
C．a＞1
D．a≥1

Answer 1

【答案】分析：将等轴双曲线x²-y²=a²与直线y=ax（a＞0）的方程联立，利用判别式小于零即可．
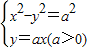
解答：解：由得（1-a²）x²=a²，
   若a=1，（1-a²）x²=a²无解，即两曲线无公共点；
   若1-a²＜0，即a＞1或a＜-1（舍），两曲线无公共点；
   综上所述，a≥1．故排除A、B、C；
故选D．
点评：本题考查直线与圆锥曲线的位置关系，解决的方法是判别式法或者是数形结合法，属于容易题．