
| 2 |
| 2 |

| x |
| a |
| y |
| b |
| |b+a-ab| | ||
|
| ab |
| ab |
| ab |
| ab |
| 2 |
| ab |
| 2 |
| ab |
| ab |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |


 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
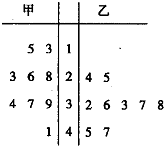 如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为
如图是甲、乙两名篮球运动员在以往几场篮球赛中得分的茎叶图,设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
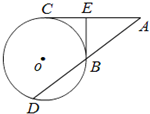 (几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB=
(几何证明选讲选做题)如图,过⊙O外一点A分别作切线AC和割线AD,C为切点,D,B为割线与⊙O的交点,过点B作⊙O的切线交AC于点E.若BE⊥AC,BE=3,AE=4,则DB=查看答案和解析>>
科目:高中数学 来源: 题型:
| A、m∥α,n∥α,则m∥n |
| B、m∥n,m∥α,则n∥α |
| C、m⊥α,m⊥β,则α∥β |
| D、α⊥γ,β⊥γ,则α∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com