
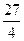 x2(1-x).
x2(1-x).  ;
; (x∈[0,+∞
(x∈[0,+∞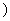 ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由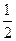 (x-1),x∈[n,n+1],则(x-n)∈[0,1]
(x-1),x∈[n,n+1],则(x-n)∈[0,1]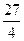 (x-n)2(1+n-x). f(x)=
(x-n)2(1+n-x). f(x)=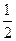 f(x-1)=
f(x-1)=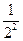 f(x-2)=…=
f(x-2)=…= f(x-n)=
f(x-n)=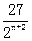 (x-n)2(1+n-x). (n=0也适用). ………………4分
(x-n)2(1+n-x). (n=0也适用). ………………4分
 (x)=
(x)=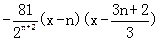 ,由f
,由f (x)=0得x=n或x=n+
(x)=0得x=n或x=n+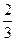
| x | n | (n,n+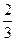 ) ) | n+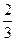 | (n+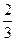 ,n+1) ,n+1) | n+1 |
f (x) (x) | | + | 0 | - | + |
| | 0 | ↗ | 极大 | ↘ | 0 |
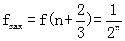 ,
, (x∈[n,n+1]).…8分
(x∈[n,n+1]).…8分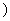 即为y=f(x),x∈[n,n+1],f
即为y=f(x),x∈[n,n+1],f (x)="-1."
(x)="-1." 
 (x)=-1在[n,n+1]上有解问题
(x)=-1在[n,n+1]上有解问题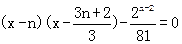 在[n,n+1]内是否有解. ……11分
在[n,n+1]内是否有解. ……11分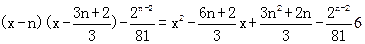 ,
, +
+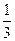 ∈[n,n+1],
∈[n,n+1],
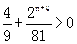 ,g(n)=
,g(n)=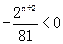 ,g(n+1)=
,g(n+1)=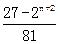 ,
,

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源:不详 题型:单选题
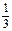 x3+
x3+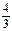 ,则过点P(2
,则过点P(2 ,4)的切线方程是 ( )
,4)的切线方程是 ( )| A.4x-y-4="0." | B.x-4y-4=0 . . |
| C.4x-4y-1="0." | D.4x+y-4=0. |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.a=1,b=1 | B.a=-1,b=1 |
| C.a=1,b=-1 | D.a=-1,b=-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com