
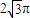 ��
��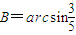 ��
��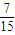
 ��������
��������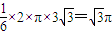 ���ʢڲ���ȷ��
���ʢڲ���ȷ��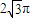 ��
��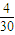 �������ij����ε����Ϊ0.2+
�������ij����ε����Ϊ0.2+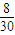 =
=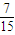 ���ʢ���ȷ��
���ʢ���ȷ��

 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ѧϰ�ܱ�����ѧ����ʦ��α�߶���(ѡ��2��2)��2009��2010ѧ�ꡡ��39�ڡ��ܵ�195�� ��ʦ��α� ���ͣ�013
�����������⣺
(1)��![]() ��0����f(x)��0��
��0����f(x)��0��
(2)![]() dx��4��
dx��4��
(3)f(x)��ԭ����ΪF(x)����F(x)����TΪ���ڵĺ�������![]() ��
��![]() ��
��
������ȷ����ĸ���Ϊ
1
2
3
0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�022
(
�Ƹ���ѧģ��)�����������⣺A.��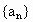 �ɵȱ����У�
�ɵȱ����У�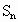 ��ǰn��ͣ���
��ǰn��ͣ���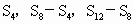 �ɵȱ����У�
�ɵȱ����У�
B.��֪����y=2sin(��x����)Ϊż����(0��������)����ͼ����ֱ��y=2�Ľ���ĺ�����Ϊ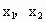 ����
����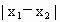 ����СֵΪ����������ֵΪ2������ֵΪ
����СֵΪ����������ֵΪ2������ֵΪ ��
��
C.����y=f(x)��ͼ����ֱ��x=a������һ�����㣻
D.����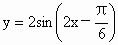 ��ͼ���һ���ԳƵ���
��ͼ���һ���ԳƵ��� ��
��
������ȷ����Ĵ�����________(����ԭ˳�������Ϊ��ȷ����Ĵ��Ŷ�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2012-2013ѧ�����ʡ������������ѧ�������ϣ��ڶ����¿���ѧ�Ծ����Ŀƣ��������棩 ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com