给出下列命题:
①函数y=f(x-2)与函数y=f(2-x)的图象关于x=2对称;
②函数y=f(x)导函数为y=f′(x),若f′(x)=0,则f(x)必为函数y=f(x)的极值;
③函数y=sinx在一象限单调递增;
④y=tanx在其定义域内为单调增函数.
其中正确的命题序号为 .
【答案】
分析:对于①根据函数y=f(a+x)与函数y=f(b-x)的图象关于直线x=
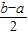
对称.得函数y=f(x+2)的图象与函数y=f(2-x)的图象关于直线x=2对称,从而进行判断.
②结合极值的定义可知,除了要求f′(x
)=0外,还的要求在两侧有单调性的改变(或导函数有正负变化),通过反例可知②不成立.
③y=sinx在第一象限有增有减.
④由正切函数的单调性可得④不正确.
解答:解:①因为函数y=f(a+x)与函数y=f(b-x)的图象关于直线x=

对称
所以函数y=f(x+2)的图象与函数y=f(2-x)的图象关于直线x=
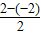
=2对称.①正确;
对于②,如f(x)=x
3,f′(x)=3x
2,f′(x)|
x=0=0,但x=0不是函数的极值点.
所以f′(x
)=0是x
为函数y=f(x)的极值点的必要不充分条件,故②不正确;
③y=sinx在第一象限有增有减,故③是假命题.
④由函数y=tanx的图象可得,它在每一个开区间(-
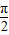
,
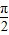
),k∈Z上都是增函数,但在它的定义域内不是增函数,故④不正确.
故答案为:①.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答,注意函数性质的灵活运用.

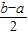 对称.得函数y=f(x+2)的图象与函数y=f(2-x)的图象关于直线x=2对称,从而进行判断.
对称.得函数y=f(x+2)的图象与函数y=f(2-x)的图象关于直线x=2对称,从而进行判断. 对称
对称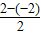 =2对称.①正确;
=2对称.①正确;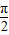 ,
,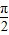 ),k∈Z上都是增函数,但在它的定义域内不是增函数,故④不正确.
),k∈Z上都是增函数,但在它的定义域内不是增函数,故④不正确.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案