
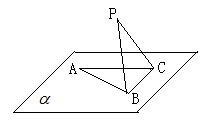
如图,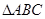 在平面
在平面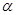 内,
内,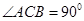 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面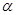 外一个动点,且PC=
外一个动点,且PC=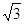 ,
,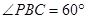
(1)问当PA的长为多少时,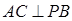
(2)当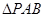 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
(1) ;(2)
;(2)
解析试题分析:(1)由分析可知当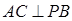 时,
时,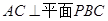 ,则
,则 ,由勾股定理可求得
,由勾股定理可求得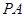 。(2)因为
。(2)因为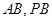 为定值,且
为定值,且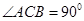 ,
,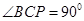 ,所以当
,所以当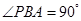 时,
时,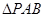 的面积取得最大值。分析可知
的面积取得最大值。分析可知 均是以
均是以 为底的等腰三角形,故取
为底的等腰三角形,故取 中点
中点 ,连接
,连接 。则有
。则有 ,从而可得
,从而可得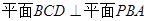 。过
。过 作
作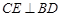 ,E为垂足,从而可得
,E为垂足,从而可得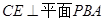 ,所以
,所以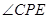 就是直线
就是直线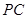 与平面
与平面 所成角,在
所成角,在 中即可求此角。
中即可求此角。
试题解析:(1)因为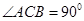 ,所以
,所以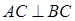 ,当
,当 时,
时,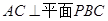 ,而
,而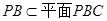 ,所以
,所以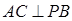 时,此时,
时,此时, ,即当
,即当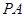 =
= 时,
时,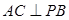
(2)
在 中,因为PC=
中,因为PC=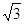 ,
,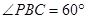 ,
, ,所以
,所以 ,
, .当
.当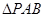 的面积取得最大值时,
的面积取得最大值时,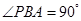 ,(如图)在
,(如图)在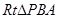 中,因为
中,因为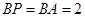 ,取
,取 中点
中点 ,连接
,连接 。因为
。因为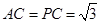 且点
且点 为
为 中点,所以
中点,所以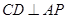 ,因为
,因为 ,所以
,所以 ,由此可求得
,由此可求得 ,又在
,又在 中,
中, ,所以
,所以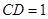 ,过
,过 作
作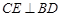 ,E为垂足,由于
,E为垂足,由于 ,所以,
,所以,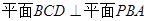 ,由两个平面互相垂直的性质可知:
,由两个平面互相垂直的性质可知: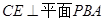 ,所以
,所以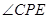 就是直线
就是直线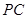 与平面
与平面 所成角,在
所成角,在 中,可求得
中,可求得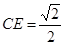 ,在
,在 中,
中,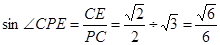 ,所以直线
,所以直线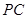 与平面
与平面 所成角的正弦值是
所成角的正弦值是 .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,底面ABCD为菱形,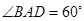 ,Q为AD的中点.
,Q为AD的中点.

(1)若PA=PD,求证:平面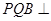 平面PAD;
平面PAD;
(2)点M在线段上,PM=tPC,试确定实数t的值,使PA//平面MQB.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图, 是圆
是圆 的直径,点
的直径,点 是圆
是圆 上异于
上异于 的点,直线
的点,直线
 分别为
分别为 的中点。
的中点。
(1)记平面 与平面
与平面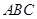 的交线为
的交线为 ,试判断
,试判断 与平面
与平面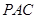 的位置关系,并加以说明;
的位置关系,并加以说明;
(2)设(1)中的直线 与圆
与圆 的另一个交点为
的另一个交点为 ,且点
,且点 满足
满足 ,记直线
,记直线
平面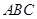 所成的角为
所成的角为 异面直线
异面直线 与
与 所成的锐角为
所成的锐角为 ,二面角
,二面角 的大小为
的大小为
①求证:
②当点 为弧
为弧 的中点时,
的中点时,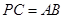 ,求直线
,求直线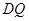 与平面
与平面 所成的角的正弦值。
所成的角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在正三棱柱ABCDEF中,AB=2,AD=1.P是CF的延长线上一点,FP=t.过A、B、P三点的平面交FD于M,交FE于N.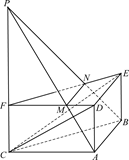
(1)求证:MN∥平面CDE;
(2)当平面PAB⊥平面CDE时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com