
(本小题满分13分)已知点P(一1, )是椭圆E:
)是椭圆E: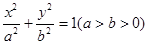 上一点F1,F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
上一点F1,F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(1)求椭圆E的方程;
(2)设A,B是椭圆E上两个动点,满足: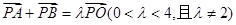 ,求直线AB的斜率
,求直线AB的斜率
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案科目:高中数学 来源: 题型:单选题
过双曲线C: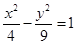 的左焦点作倾斜角为
的左焦点作倾斜角为 的直线
的直线 ,则直线
,则直线 与双曲线C的交点情况是( )
与双曲线C的交点情况是( )
| A.没有交点 |
| B.只有一个交点 |
| C.两个交点都在左支上 |
| D.两个交点分别在左、右支上 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
现从80件产品中随机抽出10件进行质量检验,下列说法正确的是( )
| A.80件产品是总体 | B.10件产品是样本 |
| C.样本容量是80 | D.样本容量是10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分10分)在1,2,---,7这7个自然数中,任取 个不同的数.
个不同的数.
(1)求这 个数中至少有
个数中至少有 个是偶数的概率;
个是偶数的概率;
(2)设 为这
为这 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为 ,则有两组相邻的数
,则有两组相邻的数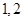 和
和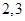 ,此时
,此时 的值是
的值是 ).求随机变量
).求随机变量 的分布列及其数学期望
的分布列及其数学期望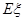 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com