
 如图所示,设 A,B,C,D是不共面的四点,P,Q,R,S分别是AC,BC,BD,AD的中点,若AB=12$\sqrt{2}$,CD=4$\sqrt{3}$,且四边形PQRS的面积是12$\sqrt{3}$,
如图所示,设 A,B,C,D是不共面的四点,P,Q,R,S分别是AC,BC,BD,AD的中点,若AB=12$\sqrt{2}$,CD=4$\sqrt{3}$,且四边形PQRS的面积是12$\sqrt{3}$,分析 (1)根据三角形的中位线的性质定理证出四边形SRQP是平行四边形,即可证明S,R,Q,P四点共面.
(2)得到∠SRQ是要求的异面直线所成的角,根据所给的条件写出角所在的三角形中的线段的长,得到要求的角的正弦值,得到结果.
解答 (1)证明:由题意知SR是△ABD的中位线,
∴SR∥$\frac{1}{2}$AB,SR=$\frac{1}{2}$AB,
同理PQ∥$\frac{1}{2}$AB,PQ=$\frac{1}{2}$AB,
∴SR∥PQ,SR=PQ,
∴四边形SRQP是平行四边形,
∴S,R,Q,P四点共面.
(2)解:由(1)可得∠SRQ是要求的异面直线所成的角,
在四边形SRQP中,SR=6$\sqrt{2}$,RQ=2$\sqrt{3}$,
四边形PQRS的面积是12$\sqrt{3}$,
∴SR上的高为$\frac{12\sqrt{3}}{6\sqrt{2}}=\sqrt{6}$
∴sin∠SRQ=$\frac{\sqrt{2}}{2}$,
∴∠SRQ=45°,
∴异面直线AB和CD所成角的大小为45°.
点评 本题考查异面直线所成的角,本题解题的过程是先做出角,再证明角是异面直线所成的角,最后求出角的大小.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
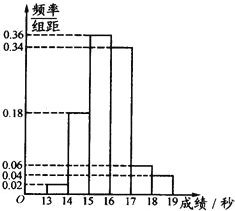 某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,如图是测试成绩频率分布直方图.成绩小于17秒的学生人数为( )
某班50名学生在一次百米测试中,成绩全部介于13秒与19秒之间,如图是测试成绩频率分布直方图.成绩小于17秒的学生人数为( )| A. | 45 | B. | 35 | C. | 17 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,4} | B. | {0,1,2,3,4,5} | C. | {2,4,7,8} | D. | {1,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “f(0)=0”是“函数f(x)是奇函数”的充要条件 | |
| B. | 命题“若$α=\frac{π}{6}$,则$sinα=\frac{1}{2}$”的否命题是“若$α≠\frac{π}{6}$,则$sinα≠\frac{1}{2}$” | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | 若p:?x0∈R,$x_0^2-{x_0}-1>0$,则?p:?x∈R,x2-x-1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com