
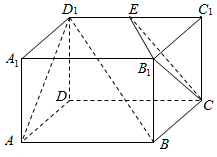
 已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.
已知长方体AC1中,AD=AB=2,AA1=1,E为D1C1的中点,如图所示.分析 (Ⅰ)连接BC1交B1C于M即可得到平面ABD1与平面B1EC的交线;
(Ⅱ)根据线面平行的判定定理即可证明:BD1∥平面B1EC;
(Ⅲ)方法1,根据几何法作出二面角的平面角即可求平面ABD1与平面B1EC所成锐二面角的大小.
方法2,建立坐标系,求出平面的法向量,利用向量法进行求解.
解答 解:(Ⅰ)连接BC1交B1C于M,则直线ME即为平面ABD1与平面B1EC的
交线,如图所示;…(4分)
(Ⅱ)由(Ⅰ)因为在长方体AC1中,所以M为BC1的中点,又E为D1C1的中点
所以在△D1C1B中EM是中位线,所以EM∥BD1,…(6分)
又EM?平面B1EC,BD1?平面B1EC,
所以BD1∥平面B1EC;…(8分)
(Ⅲ)因为在长方体AC1中,所以AD1∥BC1,
平面ABD1即是平面ABC1D1,过平面B1EC上
点B1作BC1的垂线于F,如平面图①,
因为在长方体AC1中,AB⊥平面B1BCC1,B1F?平面B1BCC1,所以B1F⊥AB,BC1∩AB=B,
所以B1F⊥平面ABD1于F.
过点F作直线EM的垂线于N,如平面图②,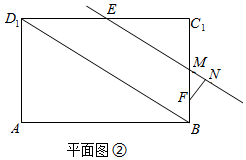
连接B1N,由三垂线定理可知,B1N⊥EM.由二面角的平面角定义可知,在Rt△B1FN中,∠B1NF即是平面ABD1与平面B1EC所成锐二面角的平面角.
因长方体AC1中,AD=AB=2,AA1=1,在平面图①中,${B_1}F=\frac{1×2}{{\sqrt{5}}}=\frac{2}{{\sqrt{5}}}$,…(10分)
$FM=\frac{{3\sqrt{5}}}{10}$,${C_1}M=\frac{{\sqrt{5}}}{2}$,C1E=1,在平面图②中,由△EMC1相似△FMN1可知$FN=\frac{{E{C_1}•FM}}{EM}$=$\frac{{1×\frac{{3\sqrt{5}}}{10}}}{{\sqrt{1+{{({\frac{{\sqrt{5}}}{2}})}^2}}}}$=$\frac{{\sqrt{5}}}{5}$,
所以tan∠B1NF=$\frac{{{B_1}F}}{NF}$=$\frac{2}{{\sqrt{5}}}•\frac{5}{{\sqrt{5}}}=2$,
所以平面ABD1与平面B1EC所成锐二面角的大小为arctan2.…(12分)
空间向量解法:
(Ⅰ)见上述.…(4分)
(Ⅱ)因为在长方体AC1中,所以DA,DC,DD1两两垂直,于是以DA,DC,DD1所在直线分别为x,y,z轴,以D为坐标原点,建立空间直角坐标系,如图所示,
因为AD=AB=2,AA1=1,所以D(0,0,0),D1(0,0,1),B(2,2,0),B1(2,2,1),C(0,2,0),E(0,1,1).所以$\overrightarrow{B{D_1}}=(-2,-2,1)$,$\overrightarrow{C{B_1}}=(2,0,1)$,$\overrightarrow{CE}=(0,-1,1)$,…(6分)
令平面B1EC的一个法向量为$\overrightarrow m=(x,y,z)$
所以$\overrightarrow{C{B_1}}⊥\overrightarrow m$,$\overrightarrow{CE}⊥\overrightarrow m$,从而有,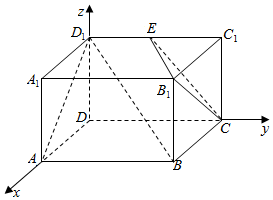
$\left\{{\begin{array}{l}{\overrightarrow{C{B_1}}•\overrightarrow m=0}\\{\overrightarrow{CE}•\overrightarrow m=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{2x+z=0}\\{y=z}\end{array}}\right.$,不妨令x=-1,
得到平面B1EC的一个法向量为$\overrightarrow m=(-1,2,2)$,
而$\overrightarrow{B{D_1}}•\overrightarrow m=2-4+2=0$,所以$\overrightarrow{B{D_1}}⊥\overrightarrow m$,又因为BD1?平面B1EC,
所以BD1∥平面B1EC.…(8分)
(Ⅲ)由(Ⅱ)知$\overrightarrow{BA}=(0,-2,0)$,$\overrightarrow{B{D_1}}=(-2,-2,1)$,令平面ABD1的一个法向量为$\overrightarrow n=(x,y,z)$,
所以$\overrightarrow{BA}⊥\overrightarrow n$,$\overrightarrow{B{D_1}}⊥\overrightarrow n$,从而有,$\left\{{\begin{array}{l}{\overrightarrow{BA}•\overrightarrow n=0}\\{\overrightarrow{B{D_1}}•\overrightarrow n=0}\end{array}}\right.$,即$\left\{{\begin{array}{l}{-2y=0}\\{-2x-2y+z=0}\end{array}}\right.$,不妨令x=1,
得到平面ABD1的一个法向量为$\overrightarrow n=(1,0,2)$,…(10分)
因为$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}$=$\frac{-1+4}{{\sqrt{9}•\sqrt{5}}}=\frac{{\sqrt{5}}}{5}$.…(11分)
所以平面ABD1与平面B1EC所成锐二面角的大小为$arccos\frac{{\sqrt{5}}}{5}$.…(12分)
点评 本题主要考查线面平行的判定以及二面角的求解,利用几何法以及建立空间坐标系,求出平面的法向量,利用向量法是解决空间二面角的常用方法,综合性较强,运算量较大.


科目:高中数学 来源: 题型:选择题
| A. | m>n | B. | m≥n | C. | m<n | D. | m≤n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m⊥l,n⊥l,则m⊥n | B. | 若m⊥l,n⊥l,则m∥n | C. | 若m⊥l,n∥l,则m⊥n | D. | 若m⊥l,n∥l,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com