
已知点S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.
|
证法 1:连结CG交DC于点H.∵ DE是△ABC的中位线,∴ DE∥AB.在△ ACG中,D是AC的中点,且DH∥AG,∴ H为CG的中点.∵ FH是△SCG的中位线,∴ FH∥SG.又  平面DEF, 平面DEF, 平面DEF, 平面DEF,
∴ SG∥平面DEF.
证法 2:∵EF为△SBC的中位线,∴ EF∥SB.∵ EF 平面SAB,SB 平面SAB,SB 平面SAB, 平面SAB,
∴ EF∥平面SAB.同理 DF∥平面SAB,EF∩DF=F,∴平面 SAB∥平面DEF.又∵ SG 平面SAB, 平面SAB,
∴ SG∥平面DEF. |
|
思路1:如图,观察图形,即可判定 SG∥平面DEF.要证明结论成立,只需证明SG与平面DEF内的一条直线平行.
观察图形可以看出:连结 CG与DE相交于H,连结FH,FH就是适合题意的直线.怎样证明 SG∥FH?只需证明H是CG的中点.思路2:要证明SG∥平面DEF,只需证明平面SAB∥平面DEF.要证明平面DEF∥平面SAB,只需证明SA∥DF,SB∥EF.而SA∥DF,SB∥EF可由题设直接推出. |


科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| QP |
| PF |
| 3x2 |
| a2 |
| 4y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:河北省正定中学2011-2012学年高二下学期第二次考试数学文科试题 题型:044
已知点M在椭圆D:![]() 上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为![]() 的正三角形.
的正三角形.
(Ⅰ)求椭圆D的方程;
(Ⅱ)设P是椭圆D上的一点,过点P的直线l交x轴于点F(-1,0),交y轴于点Q,若![]() =2
=2![]() ,求直线l的斜率;
,求直线l的斜率;
(Ⅲ)过点G(0,-2)作直线GK与椭圆N:![]() 左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|·|GK|=3|RF1|·|F1S|的直线GK是否存在?请说明理由.
左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|·|GK|=3|RF1|·|F1S|的直线GK是否存在?请说明理由.
查看答案和解析>>
科目:高中数学 来源:山东省模拟题 题型:解答题
 上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为 的正三角形,
的正三角形, ,求直线l的斜率;
,求直线l的斜率;  左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足
左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足 的直线GK是否存在?请说明理由。
的直线GK是否存在?请说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
| QP |
| PF |
| 3x2 |
| a2 |
| 4y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源:2012年山东省青岛市高考数学一模试卷(文科)(解析版) 题型:解答题
 =1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为
=1(a>b>0)上,以M为圆心的圆与x轴相切于椭圆的右焦点,若圆M与y轴相交于A,B两点,且△ABM是边长为 的正三角形.
的正三角形.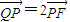 ,求直线l的斜率;
,求直线l的斜率; 左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.
左半部分交于H,K两点,又过椭圆N的右焦点F1做平行于HK的直线交椭圆N于R,S两点,试判断满足|GH|•|GK|=3|RF1|•|F1S|的直线GK是否存在?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com