
【题目】已知过点![]() 的动直线
的动直线![]() 与抛物线
与抛物线![]() :
: ![]() 相交于
相交于![]() ,
, ![]() 两点.当直线
两点.当直线![]() 的斜率是
的斜率是![]() 时,
时, ![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)设线段![]() 的中垂线在
的中垂线在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的取值范围.
的取值范围.
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)当a=3时,求A∩B;
(2)若a>0,且A∩B=![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
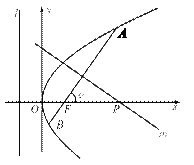
【题目】已知抛物线![]() 上一点
上一点![]() 到焦点
到焦点![]() 的距离
的距离![]() ,倾斜角
,倾斜角
为![]() 的直线经过焦点
的直线经过焦点![]() ,且与抛物线交于
,且与抛物线交于![]() 、
、![]() 两点.
两点.
(1)求抛物线的标准方程及准线![]() 的方程;
的方程;
(2)若![]() 为锐角,作线段
为锐角,作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 轴于点
轴于点![]() ,证明
,证明![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为![]() ,
,![]() ,…,
,…,![]() ).
).

(1)求成绩在![]() 的频率,并补全此频率分布直方图;
的频率,并补全此频率分布直方图;
(2)求这次考试平均分的估计值;
(3)若从成绩在![]() 和
和![]() 的学生中任选两人,求他们的成绩在同一分组区间的概率.
的学生中任选两人,求他们的成绩在同一分组区间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若点P是直线2x+y+10=0上的动点,直线PA、PB分别与圆x2+y2=4相切于A、B两点,则四边形PAOB(O为坐标原点)面积的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等比数列{an}中,a1=1,且a2是a1与a3﹣1的等差中项.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足 ![]() .求数列{bn}的前n项和
.求数列{bn}的前n项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
A.(0,﹣3)
B.(0,3)
C.(0,﹣2)
D.(0,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com