
A.(0,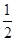 ] ] | B.[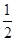 ,3] ,3] | C.[3,+∞) | D.(0,3] |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
 (单位:千克)与销售价格
(单位:千克)与销售价格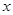 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式 其中
其中 为常数。己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数。己知销售价格为5元/千克时,每日可售出该商品11千克. 的值;
的值;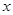 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
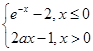 (a是常数且a>0).对于下列命题:
(a是常数且a>0).对于下列命题: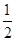 ,+∞)上恒成立,则a的取值范围是a>1;
,+∞)上恒成立,则a的取值范围是a>1;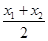 )<
)<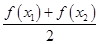 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
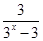 的值域为( )
的值域为( )| A.(-∞,-1) |
| B.(-1,0)∪(0,+∞) |
| C.(-1,+∞) |
| D.(-∞,-1)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.
k元.假设座位等距分布,且至少有两个座位,所有座位都视为点,且不考虑其他因素,记转盘的总造价为y元.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com