
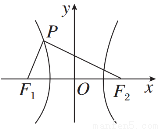
如图所示,双曲线的中心在坐标原点,焦点在x轴上,F1,F2分别为左、右焦点,双曲线的左支上有一点P,∠F1PF2=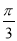 ,且△PF1F2的面积为2
,且△PF1F2的面积为2 ,双曲线的离心率为2,求该双曲线的标准方程.
,双曲线的离心率为2,求该双曲线的标准方程.
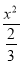 -
-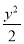 =1
=1
【解析】△PF1F2是焦点三角形,利用余弦定理来探索|PF1|,|PF2|,a,b,c之间的关系,以便确定双曲线的基本量的大小.
设双曲线方程为 -
-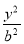 =1(a>0,b>0),则F1(-c,0),F2(c,0),在△PF1F2中,由余弦定理可得
=1(a>0,b>0),则F1(-c,0),F2(c,0),在△PF1F2中,由余弦定理可得
|F1F2|2=|PF1|2+|PF2|2-2|PF1|·|PF2|·cos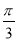 =(|PF1|-|PF2|)2+|PF1|·|PF2|,∴4c2=4a2+|PF1|·|PF2|.
=(|PF1|-|PF2|)2+|PF1|·|PF2|,∴4c2=4a2+|PF1|·|PF2|.
又S△PF1F2=2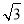 ,∴
,∴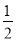 |PF1|·|PF2|·sin
|PF1|·|PF2|·sin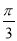 =2
=2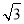 .
.
∴|PF1|·|PF2|=8,∴4c2=4a2+8,∴c2=a2+2,∴b2=c2-a2=2,又e= =2,∴c=2a,∴4a2=a2+2,∴a2=.
=2,∴c=2a,∴4a2=a2+2,∴a2=.
∴双曲线的标准方程为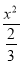 -
-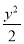 =1.
=1.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:9-2用样本估计总体(解析版) 题型:选择题
有一个容量为200的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12)内的频数为( )
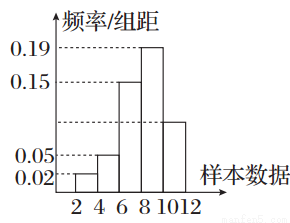
A.18 B.36 C.54 D.72
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-8曲线与方程(解析版) 题型:填空题
设抛物线C1的方程为y=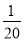 x2,它的焦点F关于原点的对称点为E.若曲线C2上的点到E、F的距离之差的绝对值等于6,则曲线C2的标准方程为________.
x2,它的焦点F关于原点的对称点为E.若曲线C2上的点到E、F的距离之差的绝对值等于6,则曲线C2的标准方程为________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-7抛物线(解析版) 题型:选择题
直线4kx-4y-k=0与抛物线y2=x交于A、B两点,若|AB|=4,则弦AB的中点到直线x+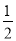 =0的距离等于( )
=0的距离等于( )
A. B.2 C.
B.2 C.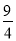 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-6双曲线(解析版) 题型:填空题
若点P在曲线C1: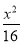 -
-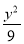 =1上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是________.
=1上,点Q在曲线C2:(x-5)2+y2=1上,点R在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-6双曲线(解析版) 题型:选择题
已知双曲线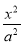 -
-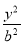 =1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
=1(a>0,b>0)的离心率为2,一个焦点与抛物线y2=16x的焦点相同,则双曲线的方程为( )
A.-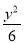 =1 B.
=1 B.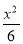 -
-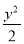 =1
=1
C.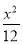 -
-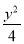 =1 D.
=1 D.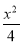 -
-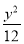 =1
=1
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-5椭圆(解析版) 题型:选择题
过点M(-2,0)的直线l与椭圆x2+2y2=2交于P1,P2,线段P1P2的中点为P.设直线l的斜率为k1(k1≠0),直线OP(O为坐标原点)的斜率为k2,则k1k2等于( )
A.-2 B.2 C.- D.
D.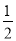
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-4直线与圆、圆与圆的位置关系(解析版) 题型:解答题
已知圆C:x2+(y-1)2=5,直线l:mx-y+1-m=0,且直线l与圆C交于A、B两点.
(1)若|AB|=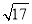 ,求直线l的倾斜角;
,求直线l的倾斜角;
(2)若点P(1,1)满足2 =
=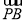 ,求此时直线l的方程.
,求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:8-2直线的交点坐标与距离公式(解析版) 题型:选择题
平面直角坐标系中,直线y=2x+1关于点(1,1)对称的直线方程是( )
A.y=2x-1 B.y=-2x+1
C.y=-2x+3 D.y=2x-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com