
圆x2+y2﹣4x=0在点P(1,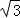 )处的切线方程为( )
)处的切线方程为( )
A. x+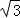 y﹣2=0 B. x+
y﹣2=0 B. x+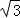 y﹣4=0 C. x﹣
y﹣4=0 C. x﹣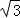 y+4=0 D. x﹣
y+4=0 D. x﹣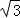 y+2=0
y+2=0
D
考点: 圆的切线方程.
专题: 计算题.
分析: 本题考查的知识点为圆的切线方程.(1)我们可设出直线的点斜式方程,联立直线和圆的方程,根据一元二次方程根与图象交点间的关系,得到对应的方程有且只有一个实根,即△=0,求出k值后,进而求出直线方程.(2)由于点在圆上,我们也可以切线的性质定理,即此时切线与过切点的半径垂直,进行求出切线的方程.
解答: 解:法一:
x2+y2﹣4x=0
y=kx﹣k+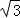 ⇒x2﹣4x+(kx﹣k+
⇒x2﹣4x+(kx﹣k+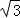 )2=0.
)2=0.
该二次方程应有两相等实根,即△=0,解得k=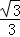 .
.
∴y﹣ =
=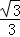 (x﹣1),
(x﹣1),
即x﹣ y+2=0.
y+2=0.
法二:
∵点(1, )在圆x2+y2﹣4x=0上,
)在圆x2+y2﹣4x=0上,
∴点P为切点,从而圆心与P的连线应与切线垂直.
又∵圆心为(2,0),∴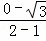 •k=﹣1.
•k=﹣1.
解得k=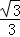 ,
,
∴切线方程为x﹣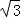 y+2=0.
y+2=0.


科目:高中数学 来源: 题型:
k棱柱有f(k)个对角面,则k+1棱柱的对角面个数f(k+1)为( )
A.f(k)+k-1 B.f(k)+k+1 C.f(k)+k D.f(k)+k-2
查看答案和解析>>
科目:高中数学 来源: 题型:
给出下列命题:
①直线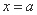 与函数
与函数 的图象至少有两个公共点;
的图象至少有两个公共点;
②函数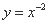 在
在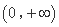 上是单调递减函数;
上是单调递减函数;
③幂函数的图象一定经过坐标原点;
④函数 (
(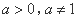 )的图象恒过定点
)的图象恒过定点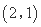 .
.
⑤设函数 存在反函数,且
存在反函数,且 的图象过点
的图象过点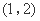 ,则函数
,则函数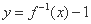
的图象一定过点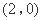 .
.
其中,真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,若b=2asinB,则这个三角形中角A的值是( )
A. 30°或60° B. 45°或60° C. 30°或120° D. 30°或150°
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}的首项a1为常数,且an+1=3n﹣2an(n∈N+).
(1)证明:{an﹣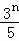 }是等比数列;
}是等比数列;
(2)若a1=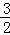 ,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(3)若{an}是递增数列,求a1的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
设偶函数f (x)=loga|x-b|在(-∞,0)上递增,则 f (a+1)与f (b+2)的大小关系是( )
f (a+1)与f (b+2)的大小关系是( )
A.f(a+1)=f (b+2) B.f (a+1)>f (b+2)
C.f(a+1)<f (b+2) D.不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com