
设数列{an}的首项a1为常数,且an+1=3n﹣2an(n∈N+).
(1)证明:{an﹣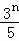 }是等比数列;
}是等比数列;
(2)若a1=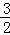 ,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(3)若{an}是递增数列,求a1的取值范围.
解答: (1)证明:因为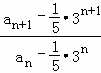 =
=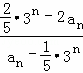 =﹣2,
=﹣2,
所以数列{an﹣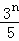 }是等比数列;
}是等比数列;
(2)解:{an﹣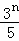 }是公比为﹣2,首项为a1﹣
}是公比为﹣2,首项为a1﹣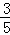 =
=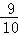 的等比数列.
的等比数列.
通项公式为an=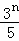 +(a1﹣
+(a1﹣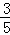 )(﹣2)n﹣1=
)(﹣2)n﹣1=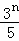 +
+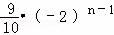
若{an}中存在连续三项成等差数列,则必有2an+1=an+an+2,
即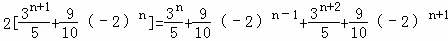
解得n=4,即a4,a5,a6成等差数列.
(3)解:如果an+1>an成立,
即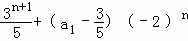 >
>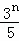 +(a1﹣
+(a1﹣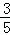 )(﹣2)n﹣1对任意自然数均成立.
)(﹣2)n﹣1对任意自然数均成立.
化简得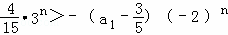 ,
,
当n为偶数时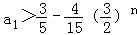 ,
,
因为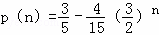 是递减数列,
是递减数列,
所以p(n)max=p(2)=0,即a1>0;
当n为奇数时,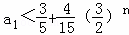 ,
,
因为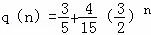 是递增数列,
是递增数列,
所以q(n)min=q(1)=1,即a1<1;
故a1的取值范围为(0,1).


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
对于定义域在R上的函数f(x),若实数x0满足f(x0)=x0,则称x0是函数f(x)的一个不动点.若函数f(x)=x2+ax+1没有不动点,则实数a的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
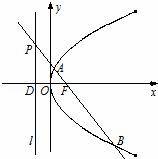
已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点.
(Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S范围;
(Ⅲ)设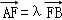 ,
,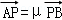 ,求证λ+μ为定值.
,求证λ+μ为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com