
已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点.
(Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S范围;
(Ⅲ)设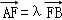 ,
,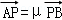 ,求证λ+μ为定值.
,求证λ+μ为定值.
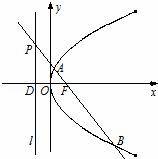
解:(Ⅰ)由题知点P,F的坐标分别为(﹣1,m),(1,0),
于是直线PF的斜率为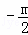 ,
,
所以直线PF的方程为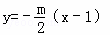 ,即为mx+2y﹣m=0.(3分)
,即为mx+2y﹣m=0.(3分)
(Ⅱ)设A,B两点的坐标分别为(x1,y1),(x2,y2),
由 得m2x2﹣(2m2+16)x+m2=0,
得m2x2﹣(2m2+16)x+m2=0,
所以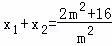 ,x1x2=1.
,x1x2=1.
于是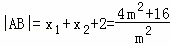 .
.
点D到直线mx+2y﹣m=0的距离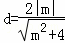 ,
,
所以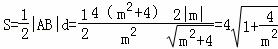 .
.
因为m∈R且m≠0,于是S>4,
所以△DAB的面积S范围是(4,+∞).(9分)
(Ⅲ)由(Ⅱ)及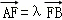 ,
,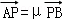 ,得(1﹣x1,﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1,m﹣y1)
,得(1﹣x1,﹣y1)=λ(x2﹣1,y2),(﹣1﹣x1,m﹣y1)
=μ(x2+1,y2﹣m),
于是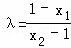 ,
,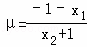 (x2≠±1).
(x2≠±1).
所以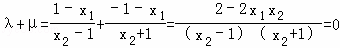 .
.
所以λ+μ为定值0.(14分)


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
已知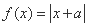 (
(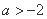 )的图象过点
)的图象过点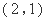 .
.
(1)求实数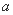 的值;
的值;
(2)如图所示的平面直角坐标系中,每一个小方格的边长均为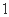 .试在该坐标系中作出函数
.试在该坐标系中作出函数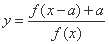 的简图,并写出(不需要证明)它的定义域、值域、奇偶性、单调区间.
的简图,并写出(不需要证明)它的定义域、值域、奇偶性、单调区间.

查看答案和解析>>
科目:高中数学 来源: 题型:
在△ABC中,若b=2asinB,则这个三角形中角A的值是( )
A. 30°或60° B. 45°或60° C. 30°或120° D. 30°或150°
查看答案和解析>>
科目:高中数学 来源: 题型:
设数列{an}的首项a1为常数,且an+1=3n﹣2an(n∈N+).
(1)证明:{an﹣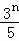 }是等比数列;
}是等比数列;
(2)若a1=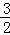 ,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
,{an}中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(3)若{an}是递增数列,求a1的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com