
(本题满分16分)定义 ,
, ,…,
,…, 的“倒平均数”为
的“倒平均数”为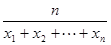 (
( ).已知数列
).已知数列 前
前 项的“倒平均数”为
项的“倒平均数”为 ,记
,记 (
( ).
).
(1)比较 与
与 的大小;
的大小;
(2)设函数 ,对(1)中的数列
,对(1)中的数列 ,是否存在实数
,是否存在实数 ,使得当
,使得当 时,
时, 对任意
对任意 恒成立?若存在,求出最大的实数
恒成立?若存在,求出最大的实数 ;若不存在,说明理由.
;若不存在,说明理由.
(3)设数列 满足
满足 ,
, (
( 且
且 ),
), (
( 且
且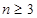 ),且
),且 是周期为
是周期为 的周期数列,设
的周期数列,设 为
为 前
前 项的“倒平均数”,求
项的“倒平均数”,求 .
.
(1)设数列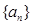 的前
的前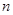 项和为
项和为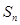 ,由题意得
,由题意得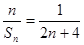 ,
,
所以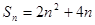 ,……(1分)
,……(1分)
当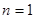 时,
时,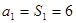 ,当
,当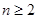 时,
时,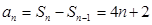 ,而
,而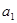 也满足此式.
也满足此式.
所以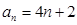 (
(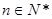 ).……(1分)
).……(1分)
所以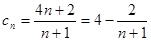 ,……(1分)
,……(1分)
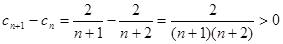 ,因此
,因此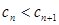 .……(1分)
.……(1分)
(2)假设存在实数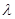 ,使得当
,使得当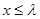 时,
时,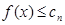 对任意
对任意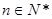 恒成立,
恒成立,
即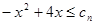 对任意
对任意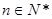 恒成立,……(2分)
恒成立,……(2分)
由(1)知数列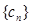 是递增数列,所以只要
是递增数列,所以只要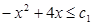 ,即
,即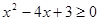 ,(2分)
,(2分)
解得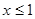 或
或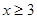 .……(1分)
.……(1分)
所以存在最大的实数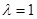 ,使得当
,使得当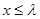 时,
时,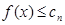 对任意
对任意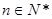 恒成立.…(1分)
恒成立.…(1分)
(3)由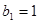 ,
,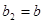 ,得
,得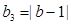 ,……(1分)
,……(1分)
① 若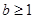 ,则
,则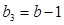 ,
,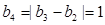 ,
,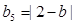 ,因为
,因为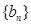 周期为
周期为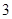 ,故
,故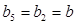 ,所以
,所以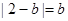 ,所以
,所以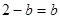 ,
,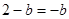 (舍),故
(舍),故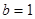 .
.
此时,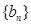 为
为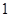 ,
,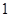 ,
, ,
,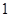 ,
,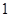 ,
, ,….符合题意.……(1分)
,….符合题意.……(1分)
② 若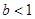 ,则
,则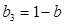 ,
,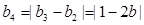 ,因为
,因为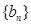 周期为
周期为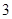 ,故
,故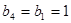 ,
,
所以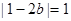 ,即
,即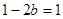 或
或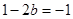 ,解得
,解得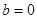 或
或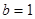 ,均不合题意.…(1分)
,均不合题意.…(1分)
设数列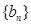 的前
的前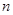 项和为
项和为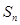 ,则对
,则对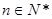 ,有
,有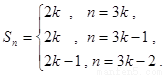 ……(1分)
……(1分)
即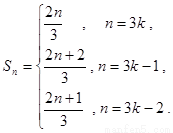 所以
所以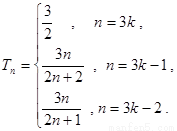 因此
因此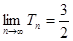 .(2分)
.(2分)
【解析】略


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源:2011-2012学年江苏省高三上学期期中考试数学 题型:解答题
(本题满分16分)A、B是函数f(x)=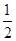 +
+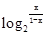 的图象上的任意两点,且
的图象上的任意两点,且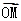 =
=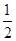 (
(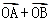 ),已知点M的横坐标为
),已知点M的横坐标为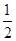 .
.
(Ⅰ)求证:M点的纵坐标为定值;
(Ⅱ)若Sn=f(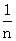 )+f(
)+f(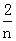 )+…+f(
)+…+f(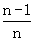 ),n∈N+且n≥2,求Sn;
),n∈N+且n≥2,求Sn;
(Ⅲ)已知数列{an}的通项公式为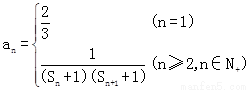 . Tn为其前n项的和,若Tn<
. Tn为其前n项的和,若Tn<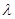 (Sn+1+1),对一切正整数都成立,求实数
(Sn+1+1),对一切正整数都成立,求实数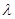 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海华师大一附中高三第二学期开学检测试题数学 题型:解答题
..(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分5分,第3小题满分6分.
已知椭圆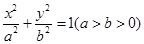 上有一个顶点到两个焦点之间的距离分别为
上有一个顶点到两个焦点之间的距离分别为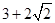 ,
,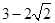 。
。
(1)求椭圆的方程;
(2)如果直线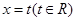 与椭圆相交于
与椭圆相交于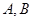 ,若
,若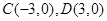 ,证明直线
,证明直线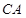 与直线
与直线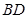 的交点
的交点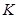 必在一条确定的双曲线上;
必在一条确定的双曲线上;
(3)过点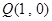 作直线
作直线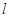 (与
(与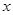 轴不垂直)与椭圆交于
轴不垂直)与椭圆交于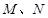 两点,与
两点,与 轴交于点
轴交于点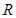 ,若
,若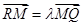 ,
,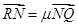 ,证明:
,证明: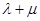 为定值。
为定值。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年上海市松江区高三5月模拟考试文科数学 题型:解答题
(本题满分16分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分
某厂生产某种零件,每个零件的成本为50元,出厂单价定为80元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.04元,但实际出厂单价最低不能低于60元。
(1)当一次订购量为多少个时,零件的实际出厂单价恰降为60元?
(2)设一次订购量为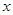 个,零件的实际出厂单价为P元,写出函数P=
个,零件的实际出厂单价为P元,写出函数P=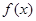 的表达式;
的表达式;
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1000个,利润又是多少元?(工厂售出一个零件的利润=实际出厂单价-成本)
查看答案和解析>>
科目:高中数学 来源:上海交通大学附属中学2012届度高二下学期期末考试数学 题型:解答题
(本题满分16分)第一题满分4分,第二题满分6分,第三题满分6分.
已知动圆过定点P(1,0),且与定直线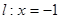 相切。
相切。
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且倾斜角为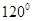 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线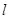 上的射影是
上的射影是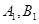 。求梯形
。求梯形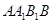 的面积;
的面积;
(3)若点C是(2)中线段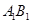 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。
查看答案和解析>>
科目:高中数学 来源:2010年上海市徐汇区高三第二次模拟考试数学卷(理) 题型:解答题
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设 、
、 为坐标平面
为坐标平面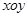 上的点,直线
上的点,直线 (
( 为坐标原点)与抛物线
为坐标原点)与抛物线 交于点
交于点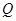 (异于
(异于 ).
).
(1)
若对任意 ,点
,点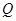 在抛物线
在抛物线 上,试问当
上,试问当 为何值时,点
为何值时,点 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程 ;
;
(2)
若点 在椭圆
在椭圆 上,试问:点
上,试问:点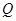 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
(3)
对(1)中点 所在圆方程
所在圆方程 ,设
,设 、
、 是圆
是圆 上两点,且满足
上两点,且满足 ,试问:是否存在一个定圆
,试问:是否存在一个定圆 ,使直线
,使直线 恒与圆
恒与圆 相切.
相切.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com