
分析 根据已知条件以线段AB所在直线为x轴,线段AB的中垂线为y轴建立平面直角坐标系,P点和M点关于原点对称,点Q在y轴上,从而设出P,M,A,B,Q的坐标:P(x,y),M(-x,-y),A(a,0),B(-a,0),Q(0,-$\sqrt{4-{a}^{2}}$),从而根据|PO|=|a|,0≤|$\overrightarrow{QM}$|<1便得到3<2y $\sqrt{4-{a}^{2}}$≤4,根据两点间距离公式从而求出|$\overrightarrow{PQ}$|2的范围,从而得出|$\overrightarrow{PQ}$|范围.
解答  解:如图,以线段AB所在直线为x轴,线段AB的中垂线为y轴,建立平面直角坐标系;设P在x轴上方,
解:如图,以线段AB所在直线为x轴,线段AB的中垂线为y轴,建立平面直角坐标系;设P在x轴上方,
|$\overrightarrow{QA}$|=|$\overrightarrow{QB}$|=2,∴Q点在y轴上;
设P(x,y),M(-x,-y),A(a,0),Q(0,-$\sqrt{4-{a}^{2}}$);
△PAB为Rt△;
∴|PO|=|a|,又0≤|$\overrightarrow{QM}$|<1;
∴$\left\{\begin{array}{l}{x}^{2}+{y}^{2}={a}^{2}\\ 0≤{x}^{2}+({y-\sqrt{4-{a}^{2}})}^{2}<1\end{array}\right.$
∴3<2y$\sqrt{4-{a}^{2}}$≤4;
|$\overrightarrow{pq}$|2=x2+(y+$\sqrt{4-{a}^{2}}$)2=2y$\sqrt{4-{a}^{2}}$+4;
∴7<|$\overrightarrow{PQ}$|2≤8;
∴$\sqrt{7}$<|$\overrightarrow{PQ}$|≤2$\sqrt{2}$;
∴|$\overrightarrow{PQ}$|的取值范围为($\sqrt{7}$,2$\sqrt{2}$].
故答案为:($\sqrt{7},2\sqrt{2}$].
点评 本题考查通过建立平面直角坐标系解决向量问题、几何问题的方法,中垂线上的点到线段两端的距离相等,关于原点对称的点的坐标的关系,以及两点间距离公式.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:解答题
 如图.四棱锥P-ABCD中,PB⊥底面ABCD.PC与平面ABCD所成角的正切值为$\frac{1}{2}$,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.
如图.四棱锥P-ABCD中,PB⊥底面ABCD.PC与平面ABCD所成角的正切值为$\frac{1}{2}$,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.
如图圆锥的轴截面为等腰直角三角形SAB,Q为底面圆周上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抛物线 | B. | 双曲线 | C. | 直线 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为梯形,AD∥BC,且AB=2BC=4,PA=AD=3,∠ABC=60°,E是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
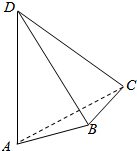 如图,AD与BC是四面体ABCD中互相垂直的棱,若BC=2,AD=4,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是$\frac{4}{3}\sqrt{11}$.
如图,AD与BC是四面体ABCD中互相垂直的棱,若BC=2,AD=4,且∠ABD=∠ACD=60°,则四面体ABCD的体积的最大值是$\frac{4}{3}\sqrt{11}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com