解:(Ⅰ) 由于曲线C
1的参数方程为:
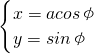
(φ为参数),
利用同角三角函数的基本关系可得
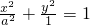
.
由于射线C
2的极坐标方程为:θ=

,故射线C
2的方程为 y=x (x≥0).
把射线的方程代入
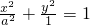
可得 x
2=
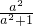
.
再由射线C
2与曲线C
1的交点的横坐标为

,可得
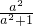
=
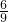
,解得 a
2=2,
故曲线C
1的普通方程为
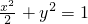
.
(Ⅱ)由|OP|•|OQ|为定值.由(Ⅰ)可知曲线C
1为椭圆,不妨设A为椭圆C
1 的上顶点,
设M(

cosθ,sinθ),P(x
P,0),Q(x
Q,0),因为直线MA与MB分别与x轴交于P、Q两点,
所以K
AM=K
AP,K
BM=K
BQ,由斜率公式并计算得 x
P=
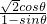
,x
Q=
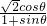
,
所以|OP|•|OQ|=|x
P•x
Q|=2,可得|OP||OQ|为定值.
分析:(I )利用三角函数知识消参,即可求得曲线的普通方程.根据极坐标与直角坐标的互化公式求得射线C
2的方程,再根据射线C
2与曲线C
1的交点的横坐标为

,求得a的值,即可得到曲线C
1的普通方程.
(Ⅱ)先设出P、Q的坐标,然后利用斜率公式求解,即可证明结论.
点评:本题主要考查同角三角函数的基本关系的应用,把参数方程化为普通方程的方法,把极坐标方程化为直角坐标
方程的方法,三点共线的性质,属于基础题.

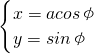 (φ为参数);射线C2的极坐标方程为:θ=
(φ为参数);射线C2的极坐标方程为:θ= ,且射线C2与曲线C1的交点的横坐标为
,且射线C2与曲线C1的交点的横坐标为
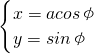 (φ为参数),
(φ为参数),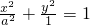 .
. ,故射线C2的方程为 y=x (x≥0).
,故射线C2的方程为 y=x (x≥0).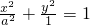 可得 x2=
可得 x2=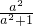 .
. ,可得
,可得 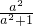 =
=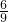 ,解得 a2=2,
,解得 a2=2,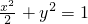 .
. cosθ,sinθ),P(xP,0),Q(xQ,0),因为直线MA与MB分别与x轴交于P、Q两点,
cosθ,sinθ),P(xP,0),Q(xQ,0),因为直线MA与MB分别与x轴交于P、Q两点,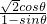 ,xQ=
,xQ=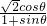 ,
, ,求得a的值,即可得到曲线C1的普通方程.
,求得a的值,即可得到曲线C1的普通方程.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.