
分析 (I)利用对数的运算性质即可得出.
(II)a${\;}^{\frac{1}{2}}}$+a${\;}^{-\frac{1}{2}}}$=3(a∈R),平方利用乘法公式化简,在平方化简代入进而得出.
解答 解:(Ⅰ)原式=$2+(-2)+\frac{1}{2}+3=\frac{7}{2}$;
(Ⅱ)∵${a^{\frac{1}{2}}}+{a^{-\frac{1}{2}}}=3$,∴a+a-1=7,∴a2+a-2=47,
∴$\frac{{{a^2}+{a^{-2}}+1}}{{a+{a^{-1}}+1}}=\frac{47+1}{7+1}=6$.
点评 本题考查了对数的运算性质、乘法公式,考查了推理能力与计算能力,属于中档题.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $5\sqrt{3}$ | B. | $10\sqrt{3}$ | C. | $\frac{5}{3}\sqrt{3}$ | D. | $\frac{10}{3}\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
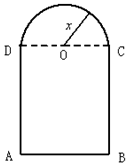 如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径
如图,用长为12m的铁丝弯成下部为矩形,上部为半圆形的框架窗户,若半圆半径查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+i | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com