
分析 (1)假设g(x)∈M,即:存在k≠0,使g(kx)=$\frac{k}{2}$+g(x)得出k=$\frac{ax}{ax-\frac{1}{2}}$,k的取值与x有关,不是常数,与假设矛盾,从而得出结论;
(2)由于当log2(kx)=$\frac{k}{2}$+log2x成立时,等价于log2k=$\frac{k}{2}$,此式显然当k=4时此式成立,可见,存在非零常数k=4,使g(kx)=$\frac{k}{2}$+g(x),从而得出答案.
解答 解:(1)假设f(x)∈M,即:存在k≠0,使f(kx)=$\frac{k}{2}$+f(x)⇒a(kx)+b=$\frac{k}{2}$+(ax+b)
⇒k=k=$\frac{ax}{ax-\frac{1}{2}}$⇒k的取值与x有关,不是常数,与假设矛盾
⇒f(x)不属于集合M
(2)log2(kx)=$\frac{k}{2}$+log2x
⇒log2k+log2x=$\frac{k}{2}$+log2x
⇒log2k=$\frac{k}{2}$,
当k=4时此式成立,
可见,存在非零常数k=4,使g(kx)=$\frac{k}{2}$+g(x)
∴g(x)∈M,
故答案为:f(x)∉M,g(x)∈M.
点评 本小题主要考查元素与集合关系的判断、对数的运算法则、对数函数的性质、方程式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
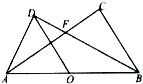 如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.
如图,△ABC与△ABD都是以AB为斜边的直角三角形,O为线段AB上一点,BD平分∠ABC,且OD∥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 6 | C. | -4或10 | D. | 0或6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2019 届的优秀学生 | B. | 高一数学必修一课本上的所有难题 | ||
| C. | 遵义四中高一年级的所有男生 | D. | 比较接近 1 的全体正数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在 x≤0,ex≤x+1 | B. | 存在 x>0,ex≤x+1 | ||
| C. | 存在 x≤0,ex>x+1 | D. | 对任意 x>0,ex≤x+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-a<3-b | B. | $\frac{b}{a}$<1 | C. | lg(a-b)>lg$\frac{1}{a-b}$ | D. | a2>b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com